Đề I
Câu 1: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng \(a\sqrt 2 \).
a) Tính thể tích của hình chóp đã cho.
b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
c) Gọi A’ và C’ lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hai hình chóp A’.ABCD và C’.CBAD bằng nhau.
Câu 2: Trong không gian tọa độ Oxyz, cho các điểm A(4; -1; 2), B(1; 2; 2) và C(1; -1; 5).
a) Chứng minh rằng ABC là tam giác đều.
b) Viết phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC) và các mặt phẳng tọa độ.
c) Viết phương trình trục của đường tròn ngoại tiếp tam giác ABC.
d) Tìm tọa độ điểm D sao cho ABCD là tứ diện đều.
Câu 1:
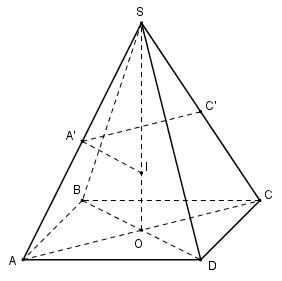
a) Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right).\)
Ta có ABCD là hình vuông cạnh a nên \(AC = BD = a\sqrt 2 \Rightarrow AO = {{a\sqrt 2 } \over 2}.\)
Xét tam giác vuông SOA có: \(SO = \sqrt {S{A^2} – O{A^2}} = \sqrt {2{a^2} – {{{a^2}} \over 2}} = {{a\sqrt 6 } \over 2}.\)
\(\eqalign{
& {S_{ABCD}} = {a^2} \cr
& \Rightarrow {V_{S.ABCD}} = {1 \over 3}SO.{S_{ABCD}} = {1 \over 3}{{a\sqrt 6 } \over 2}.{a^2} \cr&= {{{a^3}\sqrt 6 } \over 6}. \cr} \)
Gọi A’ là trung điểm của SA.
Trong (SAC) qua A’ kẻ đường thẳng vuông góc với SA cắt SO tại I.
Suy ra I là tâm mặt cầu ngoại tiếp chóp S.ABCD.
Dễ thấy
\(\eqalign{
& \Delta SA’I\,\,\text{ đồng dạng }\,\,\Delta SOA\,(g.g) \cr
& \Rightarrow {{SA} \over {SI}} = {{SO} \over {SA’}}\cr& \Rightarrow SI = {{SA.SA’} \over {SO}} = {{a\sqrt 2 .{{a\sqrt 2 } \over 2}} \over {{{a\sqrt 6 } \over 2}}} = {{a\sqrt 6 } \over 3} = R \cr} \)
Ta có A’C’ // (ABCD) \( \Rightarrow d\left( {A’;\left( {ABCD} \right)} \right) = d\left( {C’;\left( {ABCD} \right)} \right)\)
\( \Rightarrow {V_{A’.ABCD}} = {V_{C’.CBAD}}.\)
Vậy hai khối chóp A’.ABCD và C’.CBAD bằng nhau.
Câu 2:
a) Ta có:
\(\eqalign{
& \overrightarrow {AB} = \left( { – 3,3,0} \right),\cr&\overrightarrow {AC} = \left( { – 3,0,3} \right),\overrightarrow {BC} = \left( {0, – 3,3} \right) \cr
& \Rightarrow AB = \sqrt {{{\left( { – 3} \right)}^2} + {3^2} + {0^2}} = 3\sqrt 2 \cr
& AC = 3\sqrt 2 \cr
& BC = 3\sqrt 2 \cr
& \Rightarrow AB = BC = AC = 3\sqrt 2 . \cr} \)
Vậy tam giác ABC đều.
b) Ta có:
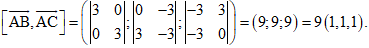
(ABC) đi qua A và nhận \(\overrightarrow n = \left( {1;1;1} \right)\) là 1 vectơ pháp tuyến nên (ABC) có phương trình: \(\left( {x – 4} \right) + \left( {y + 1} \right) + \left( {z – 2} \right) = 0 \)
\(\Leftrightarrow x + y + z – 5 = 0.\)
Mặt phẳng (ABC) cắt với trục Ox tại điểm A’(5; 0; 0)
Mặt phẳng (ABC) cắt trục Oy tại điểm B’(0; 5; 0)
Mặt phẳng (ABC) cắt trục Oz tại điểm C’(0; 0; 5).
Khi đó khối tứ diện giới hạn bởi mặt phẳng (ABC) và các mặt phẳng tọa độ là tứ diện OA’B’C’ và \({V_{OA’B’C’}} = {1 \over 6}OA’.OB’.OC’ = {1 \over 6}.5.5.5 = {{125} \over 6}.\)
c) Gọi I(a, b, c) là tâm đường tròn ngoại tiếp tam giác ABC ta có:
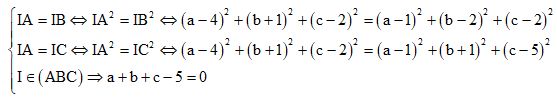
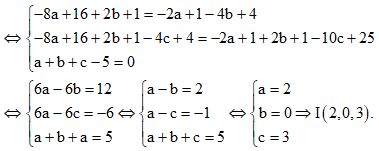
Trục của đường tròn ngoại tiếp tam giác ABC là đường thẳng đi qua I và vuông góc với (ABC) nên trục đó đi qua I(2; 0; 3) và nhận \(\overrightarrow n = \left( {1,1,1} \right)\) là 1 vectơ chỉ phương.
Do đó trục của đường tròn ngoại tiếp tam giác ABC có phương trình:
\(\left\{ \matrix{
x = 2 + t \hfill \cr
y = t \hfill \cr
z = 3 + t \hfill \cr} \right.\,\,\left( \Delta \right)\)
d) Để ABCD là tứ diện đều thì \(D \in \left( \Delta \right) \Rightarrow D\left( {2 + t,t,3 + t} \right).\)
Và \(DA = AB = 3\sqrt 2 \Leftrightarrow D{A^2} = 18.\)
\(\eqalign{
& \Leftrightarrow {\left( {t – 2} \right)^2} + {\left( {t + 1} \right)^2} + {\left( {t + 1} \right)^2} = 18 \cr
& \Leftrightarrow 3{t^2} = 12 \Leftrightarrow \left[ \matrix{
t = 2 \hfill \cr
t = – 2 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
D\left( {4,2,5} \right) \hfill \cr
D\left( {0, – 2,1} \right) \hfill \cr} \right.. \cr} \)
Vậy có hai điểm D để ABCD là tứ diện đều là \(D\left( {4,2,5} \right)\) hoặc \(D\left( {0, – 2,1} \right)\).
Đề II
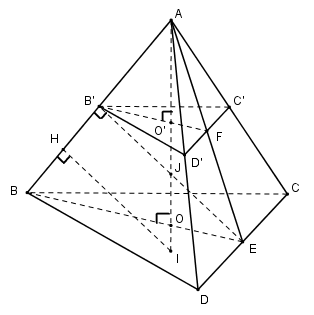
Câu 1: Cho tứ diện đều ABCD có cạnh bằng a. Gọi B’, C’, D’ lần lượt là trung điểm của các cạnh AB, AC và AD.
a) Chứng minh rằng 6 điểm B, C, D, B’, C’, D’ nằm trên một mặt cầu. Tìm bán kính của mặt cầu đó.
b) Tính thể tích khối chóp D.BCC’B’.
Câu 2: Trong không gian tọa độ Oxyz cho các điểm A(2; 0; 0), A’(6; 0; 0), B(0; 3; 0), B’(0 ;4; 0), C(0; 0; 4), C’(0; 0; 3).
a) Viết phương trình mặt cầu đi qua 4 điểm A, A’, B, C. Chứng minh rằng B’ và C’ cũng nằm trên mặt cầu đó.
b) Chứng minh rằng trực tâm H của tam giác ABC, trọng tâm G của tam giác A’B’C’ cùng nằm trên một đường thẳng đi qua O. Viết phương trình đường thẳng đó.
c) Tính khoảng cách từ điểm O tới giao tuyến của mp(ABC’) và mp(A’B’C).
Câu 1:
Advertisements (Quảng cáo)
Ta có: \(B’C’ = C’D’ = D’B’ = {a \over 2} \Rightarrow \Delta B’C’D’\) là tam giác đều cạnh \({a \over 2}.\)
Và \(AB’ = AC’ = AD’ = {a \over 2} \Rightarrow \) AB’C’D’ là tứ diện đều cạnh \({a \over 2}.\)
Gọi O và O’ lần lượt là tâm các tam giác đều BCD và B’C’D’.
Vì từ diện ABCD đều nên \(AO \bot \left( {BCD} \right)\).
Vì từ diện AB’C’D’ đều nên \(AO’ \bot \left( {B’C’D’} \right)\).
Mà (BCD) // (B’C’D’)
Gọi E là trung điểm của CD. Dễ thấy tam giác EAB cân tại E nên \(B’E \bot AB.\)
Gọi H là trung điểm của BB’, trong (ABE) kẻ đường thẳng d qua H và song song với B’E cắt AO tại I.
\( \Rightarrow HI \bot AB.\)
Ta có: \(I \in HI \Rightarrow IB = IB’\)
\(\eqalign{
& I \in OA \Rightarrow IB = IC = ID \cr
& I \in O’A \Rightarrow IB’ = IC’ = ID’ \cr} \)
Từ đó suy ra \(IB = IC = ID = IB’ = IC’ = ID’\).
Vậy điểm I cách đều 6 điểm B, C, D, B’, C’, D’ hay 6 điểm B, C, D, B’, C’, D’ cùng nằm trên mặt cầu tâm I bán kính R = IB.
Gọi \(J = B’E \cap AO.\)
Tam giác BCD đều cạnh a nên \(BE = {{a\sqrt 3 } \over 2} \Rightarrow OE = {1 \over 3}BE = {{a\sqrt 3 } \over 6}.\)
Tam giác B’C’D’ đều cạnh \({a \over 2}\) nên \(B’F = {{{a \over 2}\sqrt 3 } \over 2} = {{a\sqrt 3 } \over 4} \Rightarrow B’O’ = {2 \over 3}B’F = {{a\sqrt 3 } \over 6}.\)
Vì B’F // BE nên theo định lí Ta-let ta có: \({{B’J} \over {JE}} = {{B’O’} \over {OE}} = 1 \Rightarrow B’J = JE. \Rightarrow B’J = {1 \over 2}B’E.\)
Tam giác ACD đều cạnh a nên \(AE = {{a\sqrt 3 } \over 2},AB’ = {1 \over 2}AB = {a \over 2}.\)
Xét tam giác vuông AB’E có: \(B’E = \sqrt {A{E^2} – AB{‘^2}} = \sqrt {{{3{a^2}} \over 4} – {{{a^2}} \over 4}} = {{a\sqrt 2 } \over 2}\)
\(\Rightarrow B’J = {{a\sqrt 2 } \over 4}.\)
B’J // HI nên theo định lí Ta – let ta có: \({{B’J} \over {HI}} = {{AB’} \over {AH}} = {2 \over 3} \Rightarrow HI = {{3B’J} \over 2} = {{3{{a\sqrt 2 } \over 4}} \over 2} = {{3a\sqrt 2 } \over 8}\).
Xét tam giác vuông BHI có:
\(BI = \sqrt {B{H^2} + H{I^2}} = \sqrt {{{{a^2}} \over {16}} + {{9{a^2}} \over {32}}}\)
\( = \sqrt {{{11{a^2}} \over {32}}} = {{a\sqrt {22} } \over 8} = R.\)
b)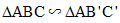 
theo tỉ số \(k = {1 \over 2} \Rightarrow {{{S_{AB’C’}}} \over {{S_{ABC}}}} = {1 \over 4} \Rightarrow {S_{BCC’B’}} = {3 \over 4}{S_{ABC}}.\)
\( \Rightarrow {{{V_{D.BCC’B’}}} \over {{V_{D.ABC}}}} = {3 \over 4} \Rightarrow {V_{D.BCC’B’}} = {3 \over 4}{V_{ABCD}}.\)
Xét tam giác vuông AOE có:
\(\eqalign{
& AO = \sqrt {A{E^2} – O{E^2}} = \sqrt {{{3{a^2}} \over 4} – {{{a^2}} \over {12}}} = {{a\sqrt 6 } \over 3}. \cr
& {S_{BCD}} = {{{a^2}\sqrt 3 } \over 4} \cr
& \Rightarrow {V_{ABCD}} = {1 \over 3}AO.{S_{BCD}} = {1 \over 3}.{{a\sqrt 6 } \over 3}.{{{a^2}\sqrt 3 } \over 4} \cr&= {{{a^3}\sqrt 2 } \over {12}}. \cr
& \Rightarrow {V_{D.BCC’B’}} = {3 \over 4}{{{a^3}\sqrt 2 } \over {12}} = {{{a^3}\sqrt 2 } \over {16}}. \cr} \)
Câu 2:
a) Gọi phương trình mặt cầu đi qua 4 điểm A, A’, B, C là \({x^2} + {y^2} + {z^2} – 2ax – 2by – 2cz + d = 0\)
\(\left( {{a^2} + {b^2} + {c^2} > 0,{a^2} + {b^2} + {c^2} > d} \right)\)
Khi đó tọa độ các điểm A, A’, B, C phải thỏa mãn phương trình mặt cầu nên ta có hệ:
\(\left\{ \matrix{
4 – 4a + d = 0 \hfill \cr
36 – 12a + d = 0 \hfill \cr
9 – 6b + d = 0 \hfill \cr
16 – 8c + d = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 4 \hfill \cr
b = {7 \over 2} \hfill \cr
c = {7 \over 2} \hfill \cr
d = 12 \hfill \cr} \right.\,\,\left( {tm} \right)\)
Vậy phương trình mặt cầu cần tìm là:\(\left( S \right):{x^2} + {y^2} + {z^2} – 8x – 7y – 7z + 12 = 0\,\,\left( * \right).\)
Thay tọa độ của điểm B’ vào (*) ta có: \(16 – 7.4 + 12 = 0 \Rightarrow B’ \in \left( S \right)\)
Thay tọa độ của điểm C’ vào (*) ta có: \(9 – 7.3 + 12 = 0 \Rightarrow C’ \in \left( S \right).\)
Gọi G là trọng tâm của tam giác A’B’C’ ta có: \(G\left( {2,{4 \over 3},1} \right).\)
\( \Rightarrow \overrightarrow {OG} = \left( {2,{4 \over 3},1} \right) = {1 \over 3}\left( {6,4,3} \right).\)
Đường thẳng d đi qua O, G nhận \(\overrightarrow u = \left( {6;4;3} \right)\) là 1 vectơ chỉ phương.
Phương trình tham số của d là
Advertisements (Quảng cáo)
\(\left\{ \matrix{
x = 6t \hfill \cr
y = 4t \hfill \cr
z = 3t \hfill \cr} \right.\)
Gọi H(x, y, z) là trực tâm của tam giác ABC ta có:
\(\left\{ \matrix{
\overrightarrow {AH} .\overrightarrow {BC} = 0 \hfill \cr
\overrightarrow {BH} .\overrightarrow {AC} = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
\left( {x – 2,y,z} \right).\left( {0, – 3,4} \right) = 0 \hfill \cr
\left( {x,y – 3,z} \right).\left( { – 2,0,4} \right) = 0 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
– 3y + 4z = 0 \hfill \cr
– 2x + 4z = 0 \hfill \cr} \right. \Leftrightarrow 2x = 3y = 4z.\)
Đặt \(2x = 3y = 4z = 12a \Rightarrow x = 6a,y = 4a,z = 3a \)
\(\Rightarrow H\left( {6a,4a,3a} \right)\)
Rõ ràng khi t = a thì \(H \in \left( d \right) \Rightarrow \)O, H, G cùng nằm trên đường thẳng có phương trình
\(\left\{ \matrix{
x = 6t \hfill \cr
y = 4t \hfill \cr
z = 3t \hfill \cr} \right.\)
c) Ta có:
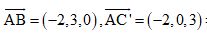
Mặt phẳng (ABC’) đi qua A và nhận \(\overrightarrow n = \left( {3,2,2} \right)\) là 1 vectơ pháp tuyến nên (ABC’) có phương trình: \(3\left( {x – 2} \right) + 2\left( {y – 0} \right) + 2\left( {z – 0} \right) = 0 \)
\(\Leftrightarrow 3x + 2y + 2z – 6 = 0.\)
Tương tự ta có:
Mặt phẳng (A’B’C) đi qua A’ và nhận \(\overrightarrow {n’} = \left( {2,3,3} \right)\) là 1 vectơ pháp tuyến nên (A’B’C) có phương trình: \(2\left( {x – 6} \right) + 3\left( {y – 0} \right) + 3\left( {z – 0} \right) = 0 \)
\(\Leftrightarrow 2x + 3y + 3z – 12 = 0.\)
Giao tuyến của 2 mặt phẳng (ABC’) và (A’B’C) là tập hợp tất cả các điểm thỏa mãn hệ phương trình:
\(\left\{ \matrix{
3x + 2y + 2z – 6 = 0 \hfill \cr
2x + 3y + 3z – 12 = 0 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
9x + 6y + 6z – 18 = 0 \hfill \cr
4x + 6y + 6z – 24 = 0 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
5x + 6 = 0 \hfill \cr
2y + 2z = 6 – 3x \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
x = – {6 \over 5} \hfill \cr
y + z = {{24} \over 5} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = – {6 \over 5} \hfill \cr
y = t \hfill \cr
z = {{24} \over 5} – t \hfill \cr} \right.\)
Vậy giao tuyến của hai mặt phẳng (ABC’) và (A’B’C) có phương trình
\(\Delta :\left\{ \matrix{
x = – {6 \over 5} \hfill \cr
y = t \hfill \cr
z = {{24} \over 5} – t \hfill \cr} \right.\).
\(\Delta \) đi qua điểm \(M\left( { – {6 \over 5};0;{{24} \over 5}} \right)\) và có vectơ chỉ phương \({\overrightarrow u _\Delta } = \left( {0,1, – 1} \right).\)
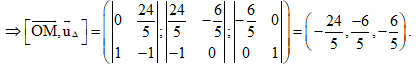
Ta có: \(d\left( {O;\Delta } \right) = {{\left| {\left[ {\overrightarrow {OM} ,{{\overrightarrow u }_\Delta }} \right]} \right|} \over {\left| {{{\overrightarrow u }_\Delta }} \right|}} = {{\sqrt {{{\left( { – {{24} \over 5}} \right)}^2} + {{\left( { – {6 \over 5}} \right)}^2} + {{\left( { – {6 \over 5}} \right)}^2}} } \over {\sqrt {{0^2} + {1^2} + {{\left( { – 1} \right)}^2}} }} \)
\(= {{{{18\sqrt 2 } \over 5}} \over {\sqrt 2 }} = {{18} \over 5}\)
Đề III
Câu 1: Cho hình hộp ABCD.A’B’C’D’. Gọi N là điểm nằm trên cạnh AB và \(\left( \alpha \right)\) là mặt phẳng đi qua ba điểm D, N, B’.
a) Mặt phẳng \(\left( \alpha \right)\) cắt hình hộp đã cho theo thiết diện là hình gì?
b) Chứng minh rằng mặt phẳng \(\left( \alpha \right)\) phân chia khối hộp đã cho thành hai khối đa diện \({H_1}\) và \({H_2}\) bằng nhau.
c) Tính tỉ số thể tích của khối đa diện \({H_1}\) và thể tích của khối tứ diện AA’BD.
Câu 2: Trong không gian tọa độ Oxyz, cho các điểm A(1; -3; -1) và B(-2; 1; 3).
a) Chứng tỏ rằng hai điểm A và B cách đều trục Ox.
b) Tìm điểm C nằm trên trục Oz sao cho tam giác ABC vuông tại C.
c) Viết phương trình hình chiếu của đường thẳng AB trên mp(Oyz).
d) Viết phương trình mặt cầu đi qua ba điểm O, A, B và có tâm nằm trên mp(Oxy).
Câu 1:
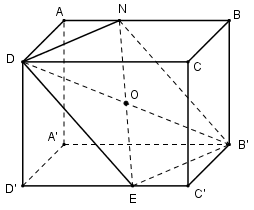
a) Giả sử \(\left( \alpha \right) \cap C’D’ = E\) thì thiết diện của hình hộp khi cắt bởi \(mp\left( \alpha \right)\) là tứ giác DNB’E.
Ta có:
\(\left\{ \matrix{
\left( \alpha \right) \cap \left( {ABCD} \right) = DN \hfill \cr
\left( \alpha \right) \cap \left( {A’B’C’D’} \right) = B’E \hfill \cr
\left( {ABCD} \right)\parallel \left( {A’B’C’D’} \right) \hfill \cr} \right. \Rightarrow DN\parallel B’E.\)
Tương tự ta có:
\(\left\{ \matrix{
\left( \alpha \right) \cap \left( {AA’B’B} \right) = {NB’} \hfill \cr
\left( \alpha \right) \cap \left( {CC’D’D} \right) = DE \hfill \cr
\left( {AA’B’B} \right)\parallel \left( {CC’D’D} \right) \hfill \cr} \right. \Rightarrow NB’\parallel DE.\)
Xét tứ giác DNB’E có: DN // B’E, NB’ // DE.
Vậy DNB’E là hình bình hành.
b) \(mp\left( \alpha \right)\) chia khối hộp thành hai khối đa diện \({H_1}:ADNA’B’ED’\) và \({H_2}:C’B’ECDNB.\)
Gọi O là giao điểm hai đường chéo B’D và NE của hình bình hành DNB’E suy ra O là trung điểm của B’D. Do đó O là tâm hình hộp ABCD.A’B’C’D’.
Gọi \({D_{(O)}}\) là phép đối xứng qua tâm O ta có:
\({D_{(O)}}\): \(A \to C’\)
\(\eqalign{
& N \to E \cr
& B’ \to D \cr
& E \to N \cr
& D’ \to B \cr
& A’ \to C \cr
& D \to B’ \cr} \)
\( \Rightarrow \)\({D_{(O)}}\): \(ADNA’B’ED’ \to C’B’ECDNB\)
hay \({D_{(O)}}\): \({H_1} \to {H_2}.\)
Mà phép đối xứng tâm O là phép dời hình nên \({V_{{H_1}}} = {V_{{H_2}}}.\)
c) Gọi \({V_{ABCD.A’B’C’D’}} = V.\)
Ta có: \({V_{AA’BD}} = {V_{A’.ABD}}.\)
\({S_{\Delta ABD}} = {1 \over 2}{S_{ABCD}} \Rightarrow {V_{A’.ABD}} = {1 \over 3}AA’.{S_{\Delta ABD}} \)
\(= {1 \over 3}.AA’.{1 \over 2}{S_{ABCD}} = {1 \over 6}{V_{ABCD.A’B’C’D’}} = {V \over 6}.\)
Mà \({V_{{H_1}}} = {V_{{H_2}}} = {V \over 2}.\)
Suy ra \({{{V_{{H_1}}}} \over {{V_{AA’BD}}}} = {{{V \over 2}} \over {{V \over 6}}} = 3.\)
Câu 2:
Ta có Ox đi qua O(0, 0, 0) và có vectơ chỉ phương \(\overrightarrow i = \left( {1,0,0} \right).\)
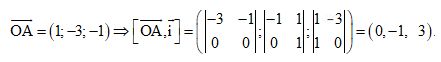
\( \Rightarrow d\left( {A;Ox} \right) = {{\left| {\left[ {\overrightarrow {OA} ,\overrightarrow i } \right]} \right|} \over {\left| {\overrightarrow i } \right|}}\)
\(= {{\sqrt {{0^2} + {{\left( { – 1} \right)}^2} + {{\left( { 3} \right)}^2}} } \over {\sqrt {{1^2} + {0^2} + {0^2}} }} = \sqrt {10} .\)
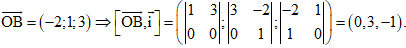
\(\eqalign{
& \Rightarrow d\left( {B;Ox} \right) = {{\left| {\left[ {\overrightarrow {OB} ,\overrightarrow i } \right]} \right|} \over {\left| {\overrightarrow i } \right|}} \cr&= {{\sqrt {{0^2} + {3^2} + {{\left( { – 1} \right)}^2}} } \over {\sqrt {{1^2} + {0^2} + {0^2}} }} = \sqrt {10} . \cr
& \Rightarrow d\left( {A;Ox} \right) = d\left( {B;Ox} \right). \cr} \)
Vậy A và B cách đều trục Ox.
b) Điểm \(C \in Oz\) nên \(C\left( {0,0,c} \right)\).
Ta có: \(\overrightarrow {AC} = \left( { – 1,3,c + 1} \right),\overrightarrow {BC} = \left( {2, – 1,c – 3} \right).\)
Tam giác ABC vuông tại C nên
\(\eqalign{
& \overrightarrow {AC} \bot \overrightarrow {BC} \cr&\Rightarrow \overrightarrow {AC} .\overrightarrow {BC} = 0 \Leftrightarrow – 2 – 3 + \left( {c + 1} \right)\left( {c – 3} \right) = 0 \cr
& \Leftrightarrow – 5 + {c^2} – 2c – 3 = 0 \cr
& \Leftrightarrow {c^2} – 2c – 8 = 0 \cr
& \Leftrightarrow \left[ \matrix{
c = 4 \hfill \cr
c = – 2 \hfill \cr} \right.. \cr} \)
Vậy có 2 điểm C thỏa mãn đề bài là \(C\left( {0,0,4} \right)\) hoặc \(C\left( {0,0, – 2} \right).\)
c) Hình chiếu của A trên mp(Oyz) là \(A’\left( {0, – 3, – 1} \right)\) và hình chiếu của B trên mp(Oyz) là \(B’\left( {0,1,3} \right)\).
\( \Rightarrow \overrightarrow {A’B’} = \left( {0,4,4} \right) = 4\left( {0,1,1} \right).\)
Suy ra hình chiếu d’ của AB trên mp(Oyz) là đường thẳng đi qua A’ và nhận \(\overrightarrow u = \left( {0,1,1} \right)\) và 1 vectơ chỉ phương.
Phương trình tham số của d’ là:
\(\left\{ \matrix{
x = 0 \hfill \cr
y = – 3 + t \hfill \cr
z = – 1 + t \hfill \cr} \right..\)
d) Gọi I là tâm của mặt cầu. Vì \(I \in \left( {Oxy} \right) \Rightarrow I\left( {a,b,0} \right).\)
Khi đó phương trình mặt cầu có dạng \({x^2} + {y^2} + {z^2} – 2ax – 2by + d = 0.\)
Vì O, A, B thuộc mặt cầu nên tọa độ của O, A, B thỏa mãn phương tình mặt cầu.
Từ đó ta có hệ phương trình:
\(\left\{ \matrix{
d = 0 \hfill \cr
1 + 9 + 1 – 2a + 6b + d = 0 \hfill \cr
4 + 1 + 9 + 4a – 2b + d = 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
d = 0 \hfill \cr
– 2a + 6b = – 11 \hfill \cr
4a – 2b = – 14 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = {{ – 53} \over {10}} \hfill \cr
b = – {{18} \over 5} \hfill \cr
d = 0 \hfill \cr} \right.\)
Vậy phương trình mặt cầu thỏa mãn đề bài là:
\({x^2} + {y^2} + {z^2} + {{53} \over 5}x + {{36} \over 5}y = 0\)
\(\Leftrightarrow 5{x^2} + 5{y^2} + 5{z^2} + 53x + 36y = 0.\)
