
1. Cho tứ diện \(ABCD\). Gọi \(M\), \(N\)lần lượt là trung điểm \(AB\) và \(CD\). Mặt phẳng \(\left( \alpha \right)\) qua \(MN\) cắt \(AD\) và \(BC\) lần lượt tại \(P\), \(Q\). Biết \(MP\)cắt \(NQ\) tại \(I\). Ba điểm nào sau đây thẳng hàng?
A. \(I\), \(A\), \(C\). B. \(I\), \(B\), \(D\).
C. \(I\), \(A\), \(B\). D. \(I\), \(C\),\(D\).
2. Cho hình chóp \(S.ABCD\) có đáy là hình thang \(ABCD\) \(\left( {AD\in BC} \right)\). Gọi \(I\) là giao điểm của \(AB\) và \(DC\), \(M\) là trung điểm \(SC\). \(DM\) cắt mặt phẳng \(\left( {SAB} \right)\) tại \(J\). Khẳng định nào sau đây sai?
A. \(S\), \(I\),\(J\) thẳng hàng.
B. \(DM \subset mp\left( {SCI} \right)\).
C. \(JM \subset mp\left( {SAB} \right)\).
D. \(SI = \left( {SAB} \right) \cap \left( {SCD} \right)\).
3. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng không có điểm chung thì chéo nhau.
B. Hai đường thẳng chéo nhau thì không có điểm chung.
C. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
D. Hai đường thẳng phân biệt không chéo nhau thì hoặc cắt nhau hoặc song song.
4. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thằng có một điểm chung thì chúng có vô số điểm chung khác.
B. Hai đường thẳng song song khi và chỉ khi chúng không điểm chung.
C. Hai đường thẳng song song khi và chỉ khi chúng không đồng phẳng.
D. Hai đường thẳng chéo nhau khi và chỉ khi chúng không đồng phẳng.
Advertisements (Quảng cáo)
5. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
B. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì trùng nhau.
C. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau hoặc trùng nhau.
D. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng lần lượt nằm trên hai mặt phẳng song song.
6. Trong các khẳng định sau, khẳng định nào đúng?
A. Hai đường thẳng chéo nhau thì chúng có điểm chung.
B. Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
C. Hai đường thẳng song song với nhau thì có thể chéo nhau.
D. Khi hai đường thẳng ở trên hai mặt phẳng phân biệt thì hai đường thẳng đó chéo nhau.
7. Cho hai đường thẳng chéo nhau và . Lấy thuộc và thuộc . Khẳng định nào sau đây đúng khi nói về hai đường thẳng và ?
Advertisements (Quảng cáo)
A. Có thể song song hoặc cắt nhau. B. Cắt nhau.
C. Song song với nhau. D. Chéo nhau.

Đáp án và lời giải chi tiết:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
B |
C |
A |
D |
C |
B |
D |
Câu1: Chọn B.
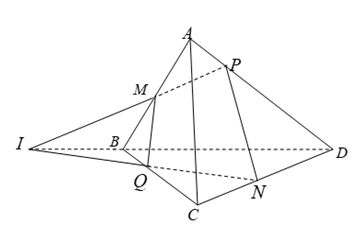
Ta có \(MP\) cắt \(NQ\) tại \(I\) \( \Rightarrow \left\{ \begin{array}{l}I \in MP\\I \in NQ\end{array} \right. \Rightarrow \left\{ \begin{array}{l}I \in \left( {ABD} \right)\\I \in \left( {CBD} \right)\end{array} \right.\).
\( \Rightarrow I \in \left( {ABD} \right) \cap \left( {CBD} \right)\).
\( \Rightarrow I \in BD\).
Vậy \(I\), \(B\), \(D\)thẳng hàng.
2. Chọn C.
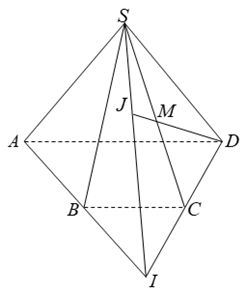
+) \(S\), \(I\), \(J\) thẳng hàng vì ba điểm cùng thuộc hai mp \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) nên A đúng.
+) \(M \in SC \Rightarrow M \in \left( {SCI} \right)\) nên \(DM \subset mp\left( {SCI} \right)\) vậy B đúng.
+) \(M \notin \left( {SAB} \right)\)nên \(JM \not\subset mp\left( {SAB} \right)\) vậy C sai.
+) Hiển nhiên D đúng theo giải thích A.
3. Chọn A. Hai đường thẳng không có điểm chung thì chúng có thể song song với nhau (khi chúng đồng phẳng) hoặc chéo nhau (khi chúng không đồng phẳng).
4. ChọnD.
+) A sai. Trong trường hợp 2 đường thẳng cắt nhau thì chúng chỉ có 1 điểm chung.
+) B và C sai. Hai đường thẳng song song khi và chỉ khi chúng đồng phằng và không có điểm chung.
5. Chọn C.
6. Chọn B.
câu 7: Chọn D.
Vì a và b chéo nhau nên bốn điểm A, B, C, D không đồng phẳng, từ đó dẫn đến AD và BC chéo nhau.

