
1. Khẳng định nào sau đây sai?
A. Nếu đường thẳng \(d \bot \left( \alpha \right)\) thì d vuông góc với hai đường thẳng trong \(\left( \alpha \right)\).
B. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
C. Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong \(\left( \alpha \right)\) thì d vuông góc với bất kì đường thẳng nào nằm trong \(\left( \alpha \right)\).
D. Nếu \(d \bot \left( \alpha \right)\) và đường thẳng a // d thì \(d \bot a\).
2. Cho hình bình hành ABCD tâm I, S là điểm nằm ngoài mặt phẳng (ABCD). Tìm mệnh đề sai .
A. \(\overrightarrow {SA} – \overrightarrow {SB} = \overrightarrow {SD} – \overrightarrow {SC} \).
B. \(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SC} + \overrightarrow {SD} \).
C. \(\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SI} \).
D. \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
3. Cho chóp S. ABCD có đáy ABCD là hình chữ nhật tâm I, cạnh bên SA vuông góc với đáy. Điểm cách đều các đỉnh của hình chóp là:
A. Trung điểm SB.
B. Trung điểm SC.
C. Trung điểm SD.
D. Điểm nằm trên đường thẳng d // SA và không thuộc SC.
4. Cho hình lập phương ABCDEFGH, góc giữa hai đường thẳng AB và GH là:
A. 00 B. 450
C. 1800 D. 900.
5. Cho hình lập phương ABCD. A’B’C’D’ . Mặt phẳng (ACC’A’) vuông góc với mặt phẳng nào sau đây:
A. (ABCD). B.(CDD’C’).
C. (BDC’). D. (A’BD).
6. Cho hình hộp ABCD. A’B’C’D’ có tất cả các cạnh bằng nhau. Điều nào sau đây sai?
A. \(AC \bot B’D’\).
B. ACC’A’ là hình thoi.
C. Cả A và B đều sai.
Advertisements (Quảng cáo)
D. Cả A và B đều đúng.
7. Cho ba đường thẳng a, b, c phân biệt cùng đi qua điểm O. Tìm câu trả lời đúng.
A. Nếu c vuông góc với a và b thì hai trong ba đường thẳng a, b, c cùng phương.
B. Nếu c vuông góc với a và b thì a, b, c không cùng nằm trong một mặt phẳng .
C. Nếu c vuông góc với a và b thì a, b, c cùng nằm trong một mặt phẳng .
D. Cà A, B, C đều sai.
8. Cho hình chóp S. ABCD có đáy là tam giác đều cạnh a, \(SA \bot (ABC)\,,SA = \dfrac{a}{2}\). Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:
A. 00 B. 450
C. 600 D. 900.
9. Trong không gian cho hai hình vuông ABCD và A’B’C’D’ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O’. Tứ giác CDD’C’ là hình gì?
A.Hình bình hành.
B. Hình vuông.
C. Hình thang.
D. Hình chữ nhật.
1.0. Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt \(\overrightarrow {AA’} = \overrightarrow a ,\,\overrightarrow {AB} = \overrightarrow b ,\,\overrightarrow {AC} = \overrightarrow c \) . Vec tơ \(\overrightarrow {B’C} \) bằng:
A.\(\overrightarrow a – \overrightarrow b – \overrightarrow c \) .
B.\(\overrightarrow c – \overrightarrow a – \overrightarrow b \) .
Advertisements (Quảng cáo)
C.\(\overrightarrow b – \overrightarrow a – \overrightarrow c \) .
D.\(\overrightarrow a + \overrightarrow b + \overrightarrow c \) .

|
Câu |
1 |
2 |
3 |
4 |
5 |
|
Đáp án |
C |
B |
B |
A |
A |
|
Câu |
6 |
7 |
8 |
9 |
10 |
|
Đáp án |
D |
B |
C |
D |
B |
2.
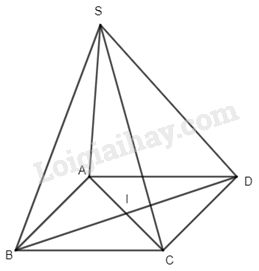
Do I là tâm hình bình hành ABCD nên \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SI} \) .
Chọn đáp án B.
3.

Ta có \(\left\{ \begin{array}{l}SA \bot BC\,\,(do\,SA \bot (ABCD))\\BA \bot BC\end{array} \right.\,\, \Rightarrow BC \bot \left( {SAB} \right)\,\, \Rightarrow BC \bot SB\) . Do đó tam giác SBC vuông tại B.
Lại có \(\left\{ \begin{array}{l}SA \bot CD\\AD \bot CD\end{array} \right.\,\, \Rightarrow CD \bot (SAD)\,\, \Rightarrow CD \bot SD\) . Do đó tam giác SDC vuông tại D.
Loại A do tam giác SBC vuông tại B nên trung điểm SB không cách đều ba điểm S, B, C.
Loại C do tam giác SCD vuông tại D nên trung điểm SD không cách đều ba điểm S, C, D.
Đáp án B đúng do tam giác SBC vuông tại B có SC là cạnh huyền nên trung điểm SC cách đều ba điểm S, B, C; do tam giác SCD vuông tại D có SC là cạnh huyền nên trung điểm SC cáchđều ba điểm S, C, D.
4.

Do ABCD.EFGH là hình lập phương nên AB // GH. Chọn đáp án A.
5.

Do ABCD.A’B’C’D’ là hình lập phương nên ta có
\(\begin{array}{l}\left\{ \begin{array}{l}AA’ \bot AD\\AA’ \bot AB\end{array} \right.\,\, \Rightarrow \,AA’ \bot (ABCD)\\AA’ \subset (ACC’A’) \Rightarrow \,\,(ABCD) \bot (ACC’A’)\end{array}\)
Vậy góc giữa (ABCD) vuông góc với (ACC’A’). Chọn đáp án A.
6.

ABCD.A’B’C’D’ là hình hộp nên các mặt đều là hình bình hành, do đó chưa đủ giả thiết để chứng minh được \(AC \bot B’D’\).
Các cạnh của hình hộp đều bằng a, tứ giác ABCD là hinh bình hành cạnh a, đường chéo có thể bằng a hoặc không bằng a nên ACC’A’ là hình bình hành , chưa chắc là hình thoi.
Vậy đáp án A và B đều là đáp án đúng. Chọn đáp án D.
8.

Hai mặt phẳng (SAC) và (SAB) có SA chung, \(SA \bot AB,\,SA \bot AC\,\, \Rightarrow \left( {(SAC),(SAB)} \right) = \left( {AB,AC} \right) = {60^0}\) .
Chọn đáp án C.
9.. Tứ giác CDD’C’ là hình bình hành. Lại có \(DC \bot \left( {ADD’} \right) \Rightarrow \,\,DC \bot DD’\) . Vậy tứ giác CDD’C’ là hình chữ nhật. Chọn đáp ánD
1.0.

Ta có \(\overrightarrow {B’C} = \overrightarrow {AC} – \overrightarrow {AB’} = \overrightarrow {AC} – \left( {\overrightarrow {AA’} + \overrightarrow {A’B’} } \right) = \overrightarrow {AC} – \overrightarrow {AA’} – \overrightarrow {AB} = \overrightarrow c – \overrightarrow a – \overrightarrow b \).
Chọn đáp án B

