
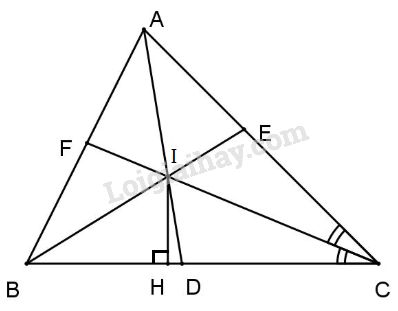
Cho tam giác ABC; các phân giác AD, BE, CF gặp nhau tại I.
a) Tính \(\widehat {IAC} + \widehat {IBC} + \widehat {IC{\rm{A}}}.\)
b) Kẻ IH vuông góc với BC (H thuộc BC). Chứng minh \(\widehat {BIH} = \widehat {CI{\rm{D}}}.\)

Advertisements (Quảng cáo)
a) Ta có \(\widehat A + \widehat B + \widehat C = {180^0}\)
\( \Rightarrow \dfrac{{\widehat A}}{2} + \dfrac{{\widehat B}}{ 2} + \dfrac{{\widehat C}}{ 2} = {90^0}\)
hay \(\widehat {IAC} + \widehat {IBC} + \widehat {ICA} = {90^0}.\)
Advertisements (Quảng cáo)
b) Từ \(\widehat A + \widehat B + \widehat C = {180^0}\)
\(\eqalign{ & \Rightarrow \widehat A + \widehat C = {180^0} – \widehat B \cr & \Rightarrow {{\widehat A} \over 2} + {{\widehat C} \over 2} = {{{{180}^0} – \widehat B} \over 2} \cr} \)
hay \(\widehat {IAC} + \widehat {ICA} = {90^0} – \dfrac{{\widehat B} }{ 2},\)
Mà \(\widehat {CI{\rm{D}}}\) là góc ngoài của \(\Delta AIC\) nên \(\widehat {CI{\rm{D}}} = \widehat {IAC} + \widehat {IC{\rm{A}}} = {90^0} -\dfrac {{\widehat B} }{ 2}\) (1).
Mặt khác \(\Delta IHB\) vuông tại H \( \Rightarrow \widehat {BIH} + \widehat {IC{\rm{A}}} = {90^0}\)
\( \Rightarrow \widehat {BIH} = {90^0} – \widehat {IBC}\) hay \(\widehat {BIH} = {90^0} – \dfrac{{\widehat B} }{ 2}\) (2)
Từ (1) và (2) \( \Rightarrow \widehat {BIH} = \widehat {CI{\rm{D}}} = {90^0} – \dfrac{{\widehat B} }{2}.\)

