
Bài 1. Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC, biết AB = 20cm, AH = 12cm, AC = 15cm. Tính BC, BH, CH.
Bài 2. Các tam giác cho dưới đây có phải là tam giác vuông không? Hãy chứng minh, nếu là tam giác vuông cho biết vuông tại đỉnh nào?
a) \(AB = 8cm;\,AC = 17cm;\,BC = 15cm.\)
b) \(AB = 25cm;\,AC = 24cm;\,BC = 6cm.\)

Advertisements (Quảng cáo)
Bài 1.
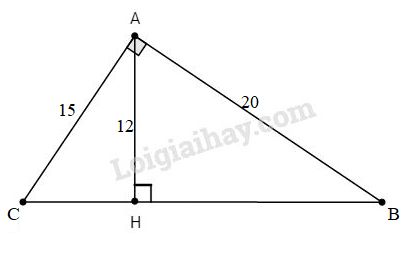
\(\Delta ABC\) vuông tại A ta có \(B{C^2} = A{B^2} + A{C^2}\)
\(\eqalign{ & = {20^2} + {15^2} \cr & = 625 \cr} \)
Advertisements (Quảng cáo)
\( \Rightarrow B{C^2} = \sqrt {625} = 25\,(cm)\)
Lại có \(AH \bot BC\) (giả thiết) nên \(\Delta AHB\) vuông tại H.
Ta có \(B{H^2} = A{B^2} + A{H^2}\)\(\, = {20^2} + {12^2} = 256\)
\( \Rightarrow BH = \sqrt {256} = 16\,(cm)\)
Do đó \(CH = BC – BH= 25 – 16 = 9\,(cm)\)
Bài 2. a) Ta có \({8^2} + {15^2} = {17^2}\,(A{B^2} + B{C^2} = C{A^2})\). Theo định lí Pytago đảo ta có \(\Delta ABC\) vuông tại B.
b) Ta có \({6^2} + {24^2} \ne {25^2}\).
Vậy \(\Delta ABC\) không phải là tam giác vuông.

