Hoạt động 1

Em thực hiện các yêu cầu sau để quy đồng mẫu hai phân số \(\dfrac{5}{6}\) và \(\dfrac{7}{4}\).
+ Tìm bội chung nhỏ nhất của hai mẫu số.
+ Viết hai phân số mới bằng hai phân số đã cho và có mẫu là số vừa tìm được.

+ Tìm bội chung nhỏ nhất của 6 và 4.
+ Lấy BNCC vừa tìm được chia cho 6. Lấy cả tử và mâu của \(\dfrac{5}{6}\) nhân với số đó.
+ Lấy BNCC vừa tìm được chia cho 4. Lấy cả tử và mâu của \(\dfrac{7}{4}\) nhân với số đó.

\(BCNN\left( {6,4} \right) = 12\)
\(\begin{array}{l}12:6 = 2\\\dfrac{5}{6} = \dfrac{{5.2}}{{6.2}} = \dfrac{{10}}{{12}}\\12:4 = 3\\\dfrac{7}{4} = \dfrac{{7.3}}{{4.3}} = \dfrac{{21}}{{12}}\end{array}\)
Hoạt động 2

Tương tự HĐ1, em hãy quy đồng mẫu hai phân số \(\dfrac{{ – 3}}{5}\) và \(\dfrac{{ – 1}}{2}\)

+ Tìm bội chung nhỏ nhất của 5 và 2.
+ Lấy BNCC vừa tìm được chia cho 5. Lấy cả tử và mâu của \(\dfrac{{ – 3}}{5}\) nhân với số đó.
+ Lấy BNCC vừa tìm được chia cho 2. Lấy cả tử và mâu của \(\dfrac{{ – 1}}{2}\) nhân với số đó.

\(BCNN\left( {5,2} \right) = 10\)
\(\begin{array}{l}10:5 = 2 = 2\\\dfrac{{ – 3}}{5} = \dfrac{{ – 3.2}}{{5.2}} = \dfrac{{ – 6}}{{10}}\\10:2 = 5\\\dfrac{{ – 1}}{2} = \dfrac{{ – 1.5}}{{2.5}} = \dfrac{{ – 5}}{{10}}\end{array}\)
Luyện tập 1

Quy đồng mẫu các phân số: \(\dfrac{{ – 3}}{4};\dfrac{5}{9};\dfrac{2}{3}\)

Để quy đồng mẫu hai hay nhiều phân số có mẫu dương, ta làm như sau:
+ Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.
+ Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.
+ Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

\(BCNN\left( {4,9,3} \right) = 36\)
Thừa số phụ: \(36:4 = 9;36:9 = 4;36:3 = 12\)
Ta có :
\(\begin{array}{l}\dfrac{{ – 3}}{4} = \dfrac{{ – 3.9}}{{4.9}} = \dfrac{{ – 27}}{{36}}\\\dfrac{5}{9} = \dfrac{{5.4}}{{9.4}} = \dfrac{{20}}{{36}}\\\dfrac{2}{3} = \dfrac{{2.12}}{{3.12}} = \dfrac{{24}}{{36}}\end{array}\)
Hoạt động 3

Em hãy nhắc lại quy tắc so sánh hai phân số có cùng mẫu (tử và mẫu đều dương), rồi so sánh hai phân số \(\dfrac{7}{{11}}\) và \(\dfrac{9}{{11}}\).

– Nhắc lại quy tắc so sánh hai phân số có cùng mẫu được học ở cấp 1
– So sánh tử của 2 phân số rồi kết luận.

Quy tắc:
Trong hai phân số có cùng mẫu, phân số nào có tử lớn hơn thì lớn hơn.
So sánh:
Ta có 7 < 9 nên \(\dfrac{7}{{11}} < \dfrac{9}{{11}}\).
Luyện tập 2

Tìm dấu thích hợp () thay cho dấu “?”


Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.

a) Ta có \( – 2 > – 7\) nên \(\dfrac{{ – 2}}{9} > \dfrac{{ – 7}}{9}\)
b) Ta có \(5 > – 10\) nên \(\dfrac{5}{7} > \dfrac{{ – 10}}{7}\)
Hoạt động 4


Để giải quyết bài toán mở đầu, ta cần so sánh \(\dfrac{3}{4}\) và \(\dfrac{5}{6}\). Em hãy thực hiện các yêu
cầu sau:
• Viết hai phân số trên về hai phân số có cùng một mẫu dương bằng cách quy đồng mẫu số.
• So sánh hai phân số cùng mẫu vừa nhận được. Từ đó kết luận về phần bánh còn
lại của hai bạn Vuông và Tròn

+ Quy đồng mẫu các phân số: \(\dfrac{3}{4}\) và \(\dfrac{5}{6}\).
+ So sánh 2 phân số cùng mẫu.

+ Quy đồng mẫu các phân số: \(\dfrac{3}{4}\) và \(\dfrac{5}{6}\):
\(\begin{array}{l}BCNN\left( {6,4} \right) = 12\\12:4 = 3\\\dfrac{3}{4} = \dfrac{{3.3}}{{4.3}} = \dfrac{9}{{12}}\\12:6 = 2\\\dfrac{5}{6} = \dfrac{{5.2}}{{6.2}} = \dfrac{{10}}{{12}}\end{array}\)
Advertisements (Quảng cáo)
So sánh 2 phân số cùng mẫu
\(\dfrac{9}{{12}} < \dfrac{{10}}{{12}}\) nên \(\dfrac{3}{4} < \dfrac{5}{6}\).
Luyện tập 3

So sánh các phân số sau:
a) \(\dfrac{7}{{10}}\) và \(\dfrac{{11}}{{15}}\)
b) \(\dfrac{{ – 1}}{8}\) và \(\dfrac{{ – 5}}{{24}}\)

Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có
cùng một mẫu dương rồi so sánh các tử với nhau: Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

a)
Ta có: \(BCNN\left( {10,15} \right) = 30\) nên
\(\begin{array}{l}\dfrac{7}{{10}} = \dfrac{{7.3}}{{10.3}} = \dfrac{{21}}{{30}}\\\dfrac{{11}}{{15}} = \dfrac{{11.2}}{{15.2}} = \dfrac{{22}}{{30}}\end{array}\)
Vì \(21 < 22\) nên \(\dfrac{{21}}{{30}} < \dfrac{{22}}{{30}}\) do đó \(\dfrac{7}{{10}} < \dfrac{{11}}{{15}}\).
b)
Ta có: \(BCNN\left( {8,24} \right) = 24\) nên
\(\dfrac{{ – 1}}{8} = \dfrac{{ – 1.3}}{{8.3}} = \dfrac{{ – 3}}{{24}}\)
Vì \( – 3 > – 5\) nên \(\dfrac{{ – 3}}{{24}} > \dfrac{{ – 5}}{{24}}\) do đó \(\dfrac{{ – 1}}{8} > \dfrac{{ – 5}}{{24}}\).
Thử thách nhỏ

Không quy đồng mẫu số, em hãy so sánh \(\dfrac{{31}}{{32}}\) và \(\dfrac{{ – 5}}{{57}}\)

+ Xác định dấu của các phân số.
+ So sánh các phân số với 0.
+ Nhận xét.

Ta có \(\dfrac{{31}}{{32}} > 0\) và \(\dfrac{{ – 5}}{{57}} < 0\) nên \(\dfrac{{31}}{{32}} > \dfrac{{ – 5}}{{57}}\).
Hoạt động 5


Viết phân số biểu thị phần bánh mỗi bạn.

+ Số bánh là tử số.
+ Số bạn là mẫu số.

Có 3 cái bánh nên tử số là 3. Chia đều cho 2 bạn nên mẫu số là 2. Vậy phân số biểu thị phần bánh mỗi bạn là: \(\dfrac{3}{2}\).
Hoạt động 6

Tròn nói mỗi bạn được 1 cái bánh và \(\dfrac{1}{2}\) cái bánh. Em có đồng ý với Tròn không?

Tìm cách chia để kiểm tra ý kiến của Tròn.

Chia đều 3 cái bánh cho 2 bạn ta chia như sau: 2 cái bánh đầu ta phân cho mỗi bạn 1 cái.
Advertisements (Quảng cáo)
Còn thừa 1 cái bánh ta chia đôi, mỗi bạn thêm \(\dfrac{1}{2}\) cái bánh. Vậy bạn Tròn đúng.
Câu hỏi

\(2\dfrac{5}{4}\) có là một hỗn số không? Vì sao?

Phần phân số của hỗn số luôn nhỏ hơn 1.

Phần phân số là \(\dfrac{5}{4} > \dfrac{4}{4} = 1\) nên \(2\dfrac{5}{4}\) không là một hồn số.
Luyện tập 4

a) Viết phân số \(\dfrac{{24}}{7}\) dưới dạng hỗn số.
b) Viết hỗn số \(5\dfrac{2}{3}\) dưới dạng phân số.

a) Chia 24 cho 7.
Phần nguyên của hỗn số là thương của phép chia.
Phần phân số của hỗn số có tử là phần dư và mẫu là 7.
b) Viết hỗn số thành phân số:
Tử = (phần nguyên) x (mẫu của phần phân số) +( tử của phần phân số)
Mẫu = mẫu của phần phân số.

a)
24=7.3+3 thương là 3 và dư là 3.
\(\dfrac{{24}}{7} = 3 + \dfrac{3}{7} = 3\dfrac{3}{7}\)
b)
\(5\dfrac{2}{3} = \dfrac{{5.3 + 2}}{3} = \dfrac{{17}}{3}\)
Giải bài 6.8 trang 12 Toán 6 tập 2

Quy đồng mẫu các phân số sau:
a) \(\dfrac{2}{3}\) và \(\dfrac{{ – 6}}{7}\)
b) \(\dfrac{5}{{{2^2}{{.3}^2}}}\) và \(\dfrac{{ – 7}}{{{2^2}.3}}\)

Để quy đồng mẫu hai hay nhiều phân số có mẫu dương, ta làm như sau:
+ Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.
+ Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.
+ Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

a) Ta có BCNN(3,7)=21
Thừa số phụ: 21:3=7 và 21:7=3
\(\dfrac{2}{3} = \dfrac{{2.7}}{{3.7}} = \dfrac{{14}}{{21}}\) và \(\dfrac{{ – 6}}{7} = \dfrac{{ – 6.3}}{{7.3}} = \dfrac{{ – 18}}{{21}}\)
b) Ta có \(BCNN\left( {\left( {{2^2}{{.3}^2}} \right),\left( {{2^2}.3} \right)} \right) = {2^2}{.3^2}\)
Thừa số phụ\(\left( {{2^2}{{.3}^2}} \right):\left( {{2^2}.3} \right) = 3\)
\(\dfrac{5}{{{2^2}{{.3}^2}}}\) và \(\dfrac{{ – 7}}{{{2^2}.3}} = \dfrac{{ – 7.3}}{{{2^2}{{.3}^2}}} = \dfrac{{ – 21}}{{{2^2}{{.3}^2}}}\)
Giải bài 6.9 trang 12 SGK Toán 6 tập 2 KNTT
Câu a
So sánh các phân số sau:
\(\dfrac{{ – 11}}{8}\) và \(\dfrac{1}{{24}}\)

So sánh với 0.

Do \(\dfrac{{ – 11}}{8} < 0\) và \(\dfrac{1}{{24}} > 0\) nên \(\dfrac{{ – 11}}{8} < \dfrac{1}{{24}}\)
Câu b
So sánh các phân số sau:
\(\dfrac{3}{{20}}\) và \(\dfrac{6}{{15}}\)

+ Rút gọn \(\dfrac{6}{{15}}\) về phân số tối giản.
+ Quy đồng phân số:
Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có
cùng một mẫu dương rồi so sánh các tử với nhau: Phân số nào có tử lớn hơn thì phân
số đó lớn hơn.

\(\dfrac{6}{{15}} = \dfrac{{6:3}}{{15:3}} = \dfrac{2}{5}\)
\(\begin{array}{l}BCNN\left( {20,5} \right) = 20\\\dfrac{2}{5} = \dfrac{{2.4}}{{5.4}} = \dfrac{8}{{20}}\\\dfrac{3}{{20}} < \dfrac{8}{{20}}\end{array}\)
Suy ra \(\dfrac{3}{{20}} < \dfrac{6}{{15}}\)
Bài 6.10 trang 12 Toán 6 tập 2

Lớp 6A có \(\dfrac{4}{5}\) học sinh thích bóng bàn, \(\dfrac{7}{{10}}\) số học sinh thích bóng đá và \(\dfrac{1}{2}\) số học sinh thích bòng chuyền. Hỏi môn thể thao nào được các bạn học sinh lớp 6A yêu thích nhất?

+ So sánh các phân số \(\dfrac{4}{5}\), \(\dfrac{7}{{10}}\) và \(\dfrac{1}{2}\).
+ Phân số nào lớn nhất thì môn tương ứng được các bạn học sinh lớp 6A yêu thích nhất.

BCNN ( 5,10,2)=10
\(\begin{array}{l}\dfrac{4}{5} = \dfrac{{4.2}}{{5.2}} = \dfrac{8}{{10}}\\\dfrac{1}{2} = \dfrac{{1.5}}{{2.5}} = \dfrac{5}{{10}}\\\dfrac{8}{{10}} > \dfrac{7}{{10}} > \dfrac{5}{{10}}\end{array}\)
Nên \(\dfrac{4}{5}\) là số lớn nhất.
Vậy môn bóng bàn được được các bạn học sinh lớp 6A yêu thích nhất.
Bài 6.11 trang 12 Toán 6 KNTT

a) Khối lượng nào lớn hơn: \(\dfrac{5}{3}kg\) hay \(\dfrac{{15}}{{11}}kg\)?
b) Vận tốc nào nhỏ hơn: \(\dfrac{5}{6}km/h\) hay \(\dfrac{4}{5}km/h\)?

a) So sánh \(\dfrac{5}{3}\) và \(\dfrac{{15}}{{11}}\)
b) So sánh \(\dfrac{5}{6}\) và \(\dfrac{4}{5}\)

a) BCNN(3,11)=33
\(\begin{array}{l}\dfrac{5}{3} = \dfrac{{5.11}}{{3.11}} = \dfrac{{55}}{{33}}\\\dfrac{{15}}{{11}} = \dfrac{{15.3}}{{11.3}} = \dfrac{{45}}{{33}}\\\dfrac{{55}}{{33}} > \dfrac{{45}}{{33}}\end{array}\)
Nên \(\dfrac{5}{3}kg > \dfrac{{15}}{{11}}kg\)
b) BCNN(6,5)=30
\(\begin{array}{l}\dfrac{5}{6} = \dfrac{{5.5}}{{6.5}} = \dfrac{{25}}{{30}}\\\dfrac{4}{5} = \dfrac{{4.6}}{{5.6}} = \dfrac{{24}}{{30}}\\\dfrac{{25}}{{30}} > \dfrac{{24}}{{30}}\end{array}\)
Nên \(\dfrac{5}{6}km/h > \dfrac{4}{5}km/h\)
Giải bài 6.12 Toán 6 tập 2 KNTT

Bảng sau cho biết chiều dài (theo đơn vị feet, 1 feet xấp xỉ bằng 30,48 cm) của một số loài động vật có vú nhỏ nhất trên thế giới.
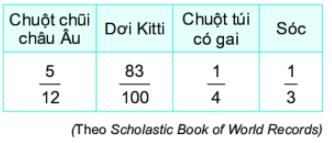
Hãy sắp xếp các động vật trên theo thứ tự chiều dài từ lớn đến bé.

So sánh \(\dfrac{5}{{12}},\dfrac{{83}}{{100}},\dfrac{1}{4},\dfrac{1}{3}\)
Sắp xếp các số theo thứ tự từ lớn đến bé.

BCNN(12,100,4,3) = 300
\(\begin{array}{l}\dfrac{5}{{12}} = \dfrac{{5.25}}{{12.25}} = \dfrac{{125}}{{300}}\\\dfrac{{83}}{{100}} = \dfrac{{83.3}}{{300.3}} = \dfrac{{249}}{{300}}\\\dfrac{1}{4} = \dfrac{{1.75}}{{4.75}} = \dfrac{{75}}{{300}}\\\dfrac{1}{3} = \dfrac{{1.100}}{{3.100}} = \dfrac{{100}}{{300}}\\\dfrac{{249}}{{300}} > \dfrac{{125}}{{300}} > \dfrac{{100}}{{300}} > \dfrac{{75}}{{300}}\end{array}\)
Do đó\(\dfrac{{83}}{{100}} > \dfrac{5}{{12}} > \dfrac{1}{3} > \dfrac{1}{4}\)
Giải bài 6.13 trang 12 SGK Toán 6

Mẹ có 15 quả táo, mẹ muốn chia đều số quả táo đó cho bốn anh em. Hỏi mỗi anh em được mấy quả táo và mấy phần của quả táo?

Mỗi người được số phần táo: số quả táo chia cho số người.
Chuyển phân số tìm được sang hỗn số.

Mỗi anh em được \(\dfrac{{15}}{4}\)quả táo.
\(\dfrac{{15}}{4} = 3 + \dfrac{3}{4} = 3\dfrac{3}{4}\)
Vậy mỗi anh em được 3 quả táo và \(\dfrac{3}{4}\) của quả táo.

