Hoạt động 1

Em hãy nhớ lại quy tắc nhân hai phân số (có tử và mẫu đều dương), rồi tính \(\dfrac{8}{3}.\dfrac{3}{7}\) và \(\dfrac{4}{6}.\dfrac{5}{8}\).

Nhân các tử với nhau và nhân các mẫu với nhau.
Rút gọn phân số.

\(\dfrac{8}{3}.\dfrac{3}{7} = \dfrac{{8.3}}{{3.7}} = \dfrac{{24}}{{21}} = \dfrac{{24:3}}{{21:3}} = \dfrac{8}{7}\)
\(\dfrac{4}{6}.\dfrac{5}{8} = \dfrac{{4.5}}{{6.8}} = \dfrac{{20}}{{48}} = \dfrac{{20:4}}{{48:4}} = \dfrac{5}{{12}}\)
Luyện tập 1

Tính:
a) \(\dfrac{{ – 2}}{5}.\dfrac{5}{4}\)
b) \(\dfrac{{ – 7}}{{10}}.\dfrac{{ – 9}}{{11}}\)

Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau.

a) \(\dfrac{{ – 2}}{5}.\dfrac{5}{4}\)\( = \dfrac{{ – 2.5}}{{5.4}} = \dfrac{{ – 10}}{{20}} = \dfrac{{ – 10:10}}{{20:10}} = \dfrac{{ – 1}}{2}\)
b) \(\dfrac{{ – 7}}{{10}}.\dfrac{{ – 9}}{{11}}\)\( = \dfrac{{ – 7.\left( { – 9} \right)}}{{10.11}} = \dfrac{{63}}{{110}}\)
Vận dụng 1

Tính diện tích hình tam giác biết một cạnh dài \(\dfrac{9}{5}cm\) , chiều cao ứng với cạnh đó bằng \(\dfrac{7}{3}cm\).

Công thức diện tích hình tam giác: Lấy chiều cao nhân độ dài cạnh rồi chia 2.

Diện tích hình tam giác: \(\dfrac{9}{5}.\dfrac{7}{3}:2 = \dfrac{{9.7.1}}{{5.3.2}} = \dfrac{{21}}{10}\left( {c{m^2}} \right)\)
Luyện tập 2

Tính:
a)\(\dfrac{6}{{13}}.\dfrac{8}{7}.\dfrac{{ – 26}}{3}.\dfrac{{ – 7}}{8}\)
b) \(\dfrac{6}{5}.\dfrac{3}{{13}} – \dfrac{6}{5}.\dfrac{{16}}{{13}}\)

a) Nhóm \(\dfrac{8}{7}\) và \(\dfrac{{ – 7}}{8}\); nhóm \(\dfrac{6}{{13}}\) và \(\dfrac{{ – 26}}{3}\).
b) Đặt \(\dfrac{6}{5}\) ra ngoài ngoặc và lấy \(\dfrac{3}{{13}}\) trừ \(\dfrac{{16}}{{13}}\).

a) \(\dfrac{6}{{13}}.\dfrac{8}{{17}}.\dfrac{{ – 26}}{3}.\dfrac{{ – 7}}{8}\)
\(\begin{array}{l} = \left( {\dfrac{6}{{13}}.\dfrac{{ – 26}}{3}} \right).\left( {\dfrac{8}{7}.\dfrac{{ – 7}}{8}} \right)\\ = \dfrac{{6.\left( { – 26} \right)}}{{13.3}}.\dfrac{{8.\left( { – 7} \right)}}{{7.8}}\\ = \dfrac{{ – 153:39}}{{39:39}}.\left( { – 1} \right)\\ = – 4.\left( { – 1} \right) = 4\end{array}\)
\(\dfrac{6}{5}.\dfrac{3}{{13}} – \dfrac{6}{5}.\dfrac{{16}}{{13}}\)
\(\begin{array}{l} = \dfrac{6}{5}.\left( {\dfrac{3}{{13}} – \dfrac{{16}}{{13}}} \right)\\ = \dfrac{6}{5}.\dfrac{{3 – 16}}{{13}}\\ = \dfrac{6}{5}.\left( { – 1} \right)\\ = \dfrac{{ – 6}}{5}\end{array}\)
Hoạt động 2

Tính các tích sau: \(\dfrac{5}{4}.\dfrac{4}{5}\); \(\dfrac{{ – 5}}{7}.\dfrac{7}{{ – 5}}\)

Lấy các tử nhân với nhau và các mẫu nhân với nhau.

\(\dfrac{5}{4}.\dfrac{4}{5} = \dfrac{{5.4}}{{4.5}} = \dfrac{{20}}{{20}} = 1\);
\(\dfrac{{ – 5}}{7}.\dfrac{7}{{ – 5}} = \dfrac{{ – 5.7}}{{7.\left( { – 5} \right)}} = \dfrac{{ – 35}}{{ – 35}} = 1\)
Câu hỏi

Từ HĐ 2, em hãy tìm phân số nghịch đảo của 11 và \(\dfrac{7}{{ – 5}}\)

Phân số nghịch đảo của số nguyên a là \(\dfrac{1}{a}\)
Phân số nghịch đảo của phân số \(\dfrac{a}{b}\left( {a,b \ne 0} \right)\) là \(\dfrac{b}{a}\)

Phân số nghịch đảo của 11 là \(\dfrac{1}{{11}}\)
Advertisements (Quảng cáo)
Phân số nghịch đảo của \(\dfrac{7}{{ – 5}}\) là \(\dfrac{{ – 5}}{7}\)
Hoạt động 3

Em hãy nhấc lại quy tắc chia hai phân số có từ và mẫu đều dương, rồi tính \(\dfrac{3}{4}:\dfrac{2}{5}\).

Chia hai phân số có tử mẫu đều dương: Lấy số bị chia nhân với số nghịch đảo của số chia.

\(\dfrac{3}{4}:\dfrac{2}{5} = \dfrac{3}{4}.\dfrac{5}{2} = \dfrac{{3.5}}{{4.2}} = \dfrac{{15}}{8}\)
Luyện tập 3

Tính:
a) \(\dfrac{{ – 8}}{9}:\dfrac{4}{3}\)
b) \(\left( { – 2} \right):\dfrac{2}{5}\)

Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.

a) \(\dfrac{{ – 8}}{9}:\dfrac{4}{3}\)
\( = \dfrac{{ – 8}}{9}.\dfrac{3}{4} = \dfrac{{ – 8.3}}{{9.4}} = \dfrac{{ – 2}}{3}\)
b) \(\left( { – 2} \right):\dfrac{2}{5}\)\( = \left( { – 2} \right).\dfrac{5}{2} = \dfrac{{ – 2.5}}{2} = – 5\)
Vận dụng 2

Trong một công thức làm bánh, An cần \(\dfrac{3}{4}\) cốc đường để làm 9 cái bánh. Nếu An chỉ muốn làm 6 cái bánh thì cần bao nhiêu cốc đường?

Tìm cốc đường làm 1 cái bánh: Lấy cốc đường chia 9.
Tìm cốc đường làm 6 cái bánh: Lấy cốc đường làm 1 cái bánh nhân với 9.

Để làm 1 cái bánh thì cần: \(\dfrac{3}{4}:9 = \dfrac{3}{4}.\dfrac{1}{9} = \dfrac{1}{{12}}\) cốc đường
Để làm 6 cái bánh thì cần: \(\dfrac{1}{{12}}.6 = \dfrac{1}{2}\) cốc đường.
Vậy để làm 6 cái bánh thì cần \(\dfrac{1}{2}\) cốc đường.
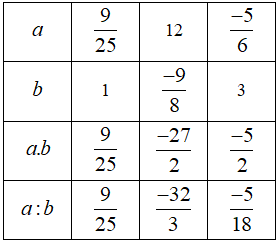
Giải bài 6.27 trang 21 Toán 6 tập 2

Thay dấu “?” bằng số thích hợp trong bảng sau:

+ Xác định a và b tương ứng cho mỗi dấu “?”.
Advertisements (Quảng cáo)
+ Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau.
+ Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.

Cột thứ hai:
\(a = \dfrac{9}{{25}},b = 1\)nên dấu “?” đầu tiên là \(a.b = \dfrac{9}{{25}}.1 = \dfrac{9}{{25}}\)
Dấu “?” thứ hai là \(a:b = \dfrac{9}{{25}}:1 = \dfrac{9}{{25}}\)
Tương tự với \(a = 12,b = \dfrac{{ – 9}}{8}\), khi đó
\(\begin{array}{l}a.b = 12.\dfrac{{ – 9}}{8} = \dfrac{{12.\left( { – 9} \right)}}{{.8}} = \dfrac{{ – 27}}{2}\\a:b = 12:\dfrac{{ – 9}}{8} = 12.\dfrac{8}{{ – 9}} = \dfrac{{12.8}}{{ – 9}} = \dfrac{{ – 32}}{3}\end{array}\)
Với \(a = \dfrac{{ – 5}}{6},b = 3\)
\(\begin{array}{l}a.b = \dfrac{{ – 5}}{6}.3 = \dfrac{{ – 5}}{2}\\a:b = \dfrac{{ – 5}}{6}:3 = \dfrac{{ – 5}}{6}.\dfrac{1}{3} = \dfrac{{ – 5}}{{18}}\end{array}\)
Vậy ta có:
Giải bài 6.28 trang 21 Toán 6 KNTT

Tính:
a) \(\dfrac{7}{8} + \dfrac{7}{8}:\dfrac{1}{8} – \dfrac{1}{2}\)
b) \(\dfrac{6}{{11}} + \dfrac{{11}}{3}.\dfrac{3}{{22}}\)

a)
Chuyển phép chia về phép nhân.
Sử dụng tính chất: \(a.b + a.c = a.\left( {b + c} \right)\)
b)
Thực hiện phép nhân trước rồi đến phép cộng.

a) \(\dfrac{7}{8} + \dfrac{7}{8}:\dfrac{1}{8} – \dfrac{1}{2}\)
\(\begin{array}{l} = \dfrac{7}{8} + \dfrac{7}{8}.8 – \dfrac{1}{2}\\ = \dfrac{7}{8}.1 + \dfrac{7}{8}.8 – \dfrac{1}{2}\\ = \left( {\dfrac{7}{8}.1 + \dfrac{7}{8}.8} \right) – \dfrac{1}{2}\\ = \dfrac{7}{8}.\left( {1 + 8} \right) – \dfrac{1}{2} = \dfrac{7}{8}.9 – \dfrac{1}{2}\\ = \dfrac{{63}}{8} – \dfrac{1}{2} = \dfrac{{63}}{8} – \dfrac{4}{8} = \dfrac{{63 – 4}}{8} = \dfrac{{59}}{8}\end{array}\)
b) \(\dfrac{6}{{11}} + \dfrac{{11}}{3}.\dfrac{3}{{22}}\)
\(\begin{array}{l} = \dfrac{6}{{11}} + \dfrac{{11.3}}{{3.22}} = \dfrac{6}{{11}} + \dfrac{1}{2}\\ = \dfrac{{12}}{{22}} + \dfrac{{11}}{{22}} = \dfrac{{12 + 11}}{{22}} = \dfrac{{23}}{{22}}\end{array}\)
Giải bài 6.29 trang 21 SGK Toán 6 tập 2

Tính một cách hợp lí:
a) \(\dfrac{3}{4}.\dfrac{1}{{13}} – \dfrac{3}{4}.\dfrac{{14}}{{13}}\)
b) \(\dfrac{5}{{13}}.\dfrac{{ – 3}}{{10}}.\dfrac{{ – 13}}{5}\)

a) Sử dụng tính chất: \(a.b – a.c = a.\left( {b – c} \right)\)
b)
+ Nhóm \(\dfrac{5}{{13}}\) với \(\dfrac{{ – 13}}{5}\) rồi tính.
+ Lấy kết quả nhân với \(\dfrac{{ – 3}}{{10}}\).

a) \(\dfrac{3}{4}.\dfrac{1}{{13}} – \dfrac{3}{4}.\dfrac{{14}}{{13}}\)
\(\begin{array}{l} = \dfrac{3}{4}.\left( {\dfrac{1}{{13}} – \dfrac{{14}}{{13}}} \right) = \dfrac{3}{4}.\left( {\dfrac{{1 – 14}}{{13}}} \right)\\ = \dfrac{3}{4}.\dfrac{{13}}{{13}} = \dfrac{3}{4}\end{array}\)
b) \(\dfrac{5}{{13}}.\dfrac{{ – 3}}{{10}}.\dfrac{{ – 13}}{5}\)
\(\begin{array}{l} = \dfrac{5}{{13}}.\dfrac{{ – 13}}{5}.\dfrac{{ – 3}}{{10}} = \left( {\dfrac{5}{{13}}.\dfrac{{ – 13}}{5}} \right).\dfrac{{ – 3}}{{10}}\\ = \dfrac{{5.\left( { – 13} \right)}}{{13.5}}.\dfrac{{ – 3}}{{10}} = \left( { – 1} \right).\dfrac{{ – 3}}{{10}} = \dfrac{3}{{10}}\end{array}\)
Bài 6.30 trang 21 Toán 6 tập 2

Mỗi buổi sáng, Nam thường đi xe đạp từ nhà đến trường với vận tốc 15 km/h và hết 20 phút. Hỏi quãng đường từ nhà Nam đến trường dài bao nhiêu ki lô mét?

Đổi thời gian phút ra giờ.
Quãng đường bằng vận tốc nhân thời gian.

20 phút = \(\dfrac{{20}}{{60}} = \dfrac{1}{3}\) giờ.
Quãng đường từ nhà Nam đến trường là: \(15.\dfrac{1}{3} = \dfrac{{15}}{3} = 5km\)
Giải bài 6.31 trang 21 Toán 6 tập 2 KNTT

Một hình chữ nhật có chiều dài là \(\dfrac{7}{2}\)cm, diện tích là \(\dfrac{{21}}{{10}}c{m^2}\). Tìm chiều rộng của hình chữ nhật

Chiều rộng hình chữ nhật bằng diện tích chia chiều dài.

Chiều rộng hình chữ nhật: \(\dfrac{{21}}{{10}}:\dfrac{7}{2} = \dfrac{{21}}{{10}}.\dfrac{2}{7} = \dfrac{{21.2}}{{10.7}} = \dfrac{3}{5}cm\)
Bài 6.32 trang 21 Toán 6 tập 2 kết nối tri thức

Tìm x, biết:
a) \(x.\dfrac{7}{2} = \dfrac{7}{9}\) ;
b) \(x:\dfrac{8}{5} = \dfrac{5}{2}\)

a) Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
b) Muốn tìm số bị chia ta lấy thương nhân với số chia.

a)
\(x.\dfrac{7}{2} = \dfrac{7}{9}\)
\(\begin{array}{l}x = \dfrac{7}{9}:\dfrac{7}{2}\\x = \dfrac{7}{9}.\dfrac{2}{7}\\x = \dfrac{{7.2}}{{9.7}}\\x = \dfrac{2}{9}\end{array}\)
b)
\(\begin{array}{l}x:\dfrac{8}{5} = \dfrac{5}{2}\\x = \dfrac{5}{2}.\dfrac{8}{5}\\x = \dfrac{{5.8}}{{2.5}}\\x = 4\end{array}\)
Giải bài 6.33 trang 21 Toán 6 tập 2

Lớp 6A có \(\dfrac{1}{3}\) số học sinh thích môn Toán. Trong số các học sinh thích môn Toán, có \(\dfrac{1}{2}\) số học sinh thích môn Ngữ văn. Hỏi có bao nhiêu phần số học sinh lớp 6A thích cả môn Toán và Ngữ văn?

Tính số phần học sinh thích môn Ngữ văn trong lớp 6A.
Thích 2 môn = thích môn Toán + thích môn Ngữ văn.

Số học sinh thích môn Ngữ văn bằng \(\dfrac{1}{2}\)số học sinh thích môn Toán nên số 1phần học sinh thích môn Ngữ văn trong lớp 6A là: \(\dfrac{1}{2}.\dfrac{1}{3} = \dfrac{{1.1}}{{2.3}} = \dfrac{1}{6}\) học sinh lớp 6A
Số phần số học sinh lớp 6A thích cả môn Toán và Ngữ văn là:
\(\dfrac{1}{3} + \dfrac{1}{6} = \dfrac{2}{6} + \dfrac{1}{6} = \dfrac{3}{6} = \dfrac{1}{2}\) học sinh lớp 6A.
Vậy lớp 6A có \(\dfrac{1}{2}\) số học sinh thích cả 2 môn.