Câu 4.1: Cho đường tròn tâm O bán kính R. Lấy ba điểm bất kỳ A, B, C trên đường tròn (O). Điểm E bất kỳ thuôc đoạn thẳng AB (và không trùng với A, B). Đường thẳng d đi qua điểm E và vuông góc với đường thẳng OA cắt đoạn thẳng AC tại điểm F. Chứng minh \(\widehat {BCF} + \widehat {BEF} = {180^0}\).
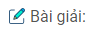
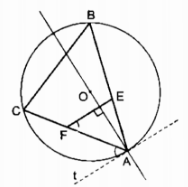
Kẻ tiếp tuyến At của đường tròn (O)
At \( \bot OA\) (tính chất tiếp tuyến)
\(EF \bot OA\) (gt)
Suy ra: At // EF
\(\widehat {EFA} = \widehat {CAt}\) (so le trong)
\(\widehat {CBA} = \widehat {CAt}\) (hệ quả góc giữa tia tiếp tuyến và dây cung)
Suy ra: \(\widehat {EFA} = \widehat {CBA}\) hay \(\widehat {EFA} = \widehat {CBE}\)
\(\widehat {EFA} + \widehat {EFC} = {180^0}\) (hai góc kề bù)
Advertisements (Quảng cáo)
\(\overparen{CBE}\) + \(\overparen{EFC}\) = 1800 (1)
Trong tứ giác BCFE ta có:
\(\overparen{BCF}\) + \(\overparen{BEF}\) + \(\overparen{CBE}\) + \(\overparen{CFE}\) = 3600 (tổng các góc trong tứ giác) (2)
Từ (1) và (2) suy ra: \(\widehat {BCF} + \widehat {BEF} = {180^0}\)
Câu 4.2: Cho tam giác ABC vuông ở A, AH và AM tương ứng là đường cao và đường trung tuyến kẻ từ A của tam giác đó. Qua điểm A kẻ đường thẳng mn vuông góc với AM. Chứng minh: AB và AC tương ứng là tia phân giác của các góc tạo bở AH và hai tia Am, An của đường thẳng mn.
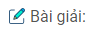
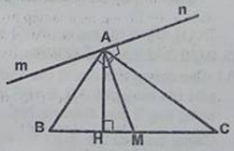
Advertisements (Quảng cáo)
∆ABCvuông tại A, có AM là đường trung tuyến ứng với cạnh huyền BC
\( \Rightarrow AM = MB = MC = {1 \over 2}BC\) (tính chất tam giác vuông)
\( \Rightarrow \) ∆AMB cân tại M
\( \Rightarrow \widehat B = \widehat {BAM}\) (1)
\(mn \bot AM\) (gt)
\( \Rightarrow \widehat {mAM} + \widehat {BAM} = {90^0}\) (2)
∆AHB vuông tại H
\( \Rightarrow \widehat B + \widehat {BAH} = {90^0}\) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {mAB} = \widehat {BAH}\). Vậy AB là tia phân giác của \(\widehat {mAH}\).
∆AMC cân tại M \( \Rightarrow \widehat {MAC} = \widehat C\) (4)
\(mn \bot AM\) (gt) \( \Rightarrow \widehat {MAC} + \widehat {nAC} = {90^0}\) (5)
∆AHC vuông tại H \( \Rightarrow \widehat {HAC} + \widehat C = {90^0}\) (6)
Từ (4), (5) và (6) suy ra: \(\widehat {HAC} = \widehat {nAC}\). Vậy AC là tia phân giác của \(\widehat {HAn}\)

