Câu 28: Các điểm \({A_1},{A_2},…,{A_{19}},{A_{20}}\) được sắp xếp theo thứ tự đó trên đường tròn (O) và chia đường tròn thành 20 cung bằng nhau. Chứng minh rằng dây \({A_1}{A_8}\) vuông góc với dây \({A_3}{A_{16}}\).
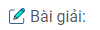
Đường tròn (O) được chia thành 20 cung bằng nhau nên số đo mỗi cung bằng
3600: 20 = 180.
Gọi giao điểm của A1A8 và A3A16 là I.
Ta có: sđ \(\overparen{{A_1}{A_3}}\) \( = {2.18^0} = {36^0}\)
\(\overparen{{A_8}{A_16}}\) \( = {8.18^0} = {144^0}\)
Ta có: \(\widehat {{A_1}I{A_3}} = {1 \over 2}\) sđ \(\overparen{{A_1}{A_3}}\) + sđ \(\overparen{{A_8}{A_16}}\) (góc có đỉnh ở trong đường tròn (O))
\( \Rightarrow \) \(\widehat {{A_1}I{A_3}} = {{36^\circ + 144^\circ } \over 2} = 90^\circ \)
\( \Rightarrow \) A1A8⊥ A3A16
Câu 29: Cho tam giác ABC vuông góc ở A. Đường tròn đường kính AB cắt BC ở D. Tiếp tuyến ở D cắt AC ở P. Chứng minh PD = PC.
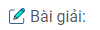
Trong đường tròn (O) ta có \(\widehat C\) là góc có đỉnh ở ngoài đường tròn.
\(\widehat C = {1 \over 2}\) (sđ \(\overparen{AmB}\) – sđ \(\overparen{AD}\)) (tính chất góc có đỉnh ở ngoài đường tròn)
mà sđ \(\overparen{AmB}\) = sđ \(\overparen{ADB}\) = 1800
Advertisements (Quảng cáo)
\(\widehat C = {1 \over 2}\) (sđ \(\overparen{ADB}\) – sđ \(\overparen{AD}\)) = \( {1 \over 2}\) (sđ \(\overparen{AD}\) + sđ \(\overparen{DB}\) – sđ \(\overparen{AD}\))= \( {1 \over 2}\) sđ \(\overparen{BD}\) (1)
\(\widehat {CDP} = \widehat {BDx}\) (đối đỉnh) (2)
\(\widehat {BDx} = {1 \over 2}\) sđ \(\overparen{BD}\) (góc giữa tia tiếp tuyến và dây cung) (3)
Từ (1), (2) và (3) suy ra: \(\widehat C = \widehat {CDP} \Rightarrow \Delta PCD\) cân tại P. Vậy PD = PC
Câu 30: Hai dây cung AB và CD kéo dài cắt nhau tại điểm E ở ngoài đường tròn (O) (B nằm giữa A và E, C nằm giữa D và E). Cho biết \(\widehat {CDE}\) = 75 0, \(\widehat {CED} = {22^0}\), \(\widehat {AOD} = {144^0}\).
Chứng minh \(\widehat {AOB} = \widehat {BAC}\).
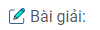
Trong đường tròn (O) ta có là góc có đỉnh ở ngoài đường tròn.
\(\widehat E = {1 \over 2}\) (sđ \(\overparen{AD}\) – sđ \(\overparen{BC}\))
sđ \(\overparen{AD}\) = \(\widehat {AOD} = 144^\circ \)
Advertisements (Quảng cáo)
\( \Rightarrow \) 22º = \({{144^\circ – sđ \overparen{BC}} \over 2}\)
Þ sđ \(\overparen{BC}\)= 144º – 2. 22º = 100º
\(\widehat {BAC} = {1 \over 2}\) sđ \(\overparen{BC}\)(tính chất nội tiếp)
\( \Rightarrow \) \(\widehat {BAC} = {1 \over 2}.100^\circ = 50^\circ \)
Trong ∆ABC ta có \(\widehat {CBE}\) là góc ngoài tại đỉnh B.
\( \Rightarrow \) \(\widehat {CBE} = \widehat {BAC} + \widehat {ACB}\) (tính chất góc ngoài của tam giác)
\( \Rightarrow \) \(\widehat {ACB} = \widehat {CBE} – \widehat {BAC} = 75^\circ – 50^\circ = 25^\circ \)
\(\widehat {ACB} = {1 \over 2}\widehat {AOB}\) (hệ quả góc nội tiếp)
\(\widehat {AOB} = 2.\widehat {ACB} = 50^\circ \)
Vậy \(\widehat {AOB} = \widehat {BAC} = 50^\circ \)
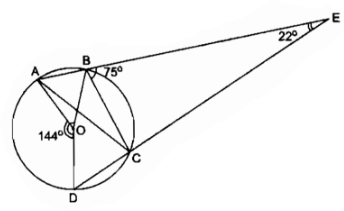
Câu 31: A, B, C là ba điểm thuộc đường tròn (O) sao cho tiếp tuyến tại A cắt tia BC tại D. Tia phân giác của \(\widehat {BAC}\) cắt đường tròn ở M, tia phân giác của \(\widehat D\) cắt AM ở I. Chứng minh DI \( \bot AM\).
\(\widehat {BAM} = \widehat {MAC}\) (vì AM là tia phân giác của \(\widehat {BAC}\))
\( \Rightarrow \widehat {BM} =\) \(\overparen{CM}\) (1)
Ta có: \(\widehat {DAM} = {1 \over 2}\) sđ \(\overparen{ACM}\) (góc giữa tia tiếp tuyến và dây cung)
Hay \(\widehat {DAM} = {1 \over 2}\) (sđ \(\overparen{AC}\) + sđ \(\overparen{CM}\) ) (2)
Gọi N là giao điểm của AM và BC.
Ta có: \(\widehat {ANC}\) là góc có đỉnh ở trong đường tròn (O).
\( \Rightarrow \) \(\widehat {ANC} = {1 \over 2}\) (sđ \(\overparen{AC}\) + sđ \(\overparen{BM}\) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {DAM} = \widehat {ANC}\) hay \(\widehat {DAN} = \widehat {AND}\)
Suy ra: ∆DAN cân tại D có DI là tia phân giác nên suy ra DI là đường cao
\( \Rightarrow \) DI ⊥ AN hay DI ⊥ AM

