Câu 38: Cho đường tròn (O) bán kính bằng 2cm. Một đường thẳng đi qua điểm A nằm bên ngoài đường tròn và cắt đường tròn tại B và C, trong đó AB = BC. Kẻ đường kính COD. Tính độ dài AD.
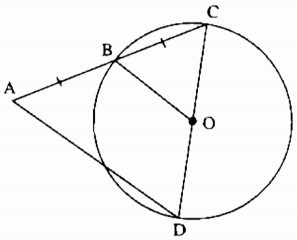
Trong tam giác ACD, ta có:
B là trung điểm của AC (gt)
O là trung điểm của CD
Nên OB là đường trung bình của ∆ACD.
Suy ra: \(OB = {1 \over 2}AD\) ( tính chất đường trung bình của tam giác)
Vậy AD = 2. OB = 2.2 = 4 (cm).
Câu 39: Cho hình thang vuông ABCD \(\widehat A = \widehat D = 90^\circ )\), AB = 4cm, BC = 13cm, CD = 9cm.
a) Tính độ dài AD.
b) Chứng minh rằng đường thẳng AD tiếp xúc với đường tròn có đường kính là BC.
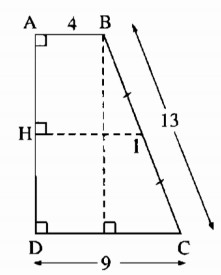
a) Kẻ BE ⊥ CD
Suy ra tứ giác ABED là hình hình chữ nhật
Ta có: AD = BE
Advertisements (Quảng cáo)
AB = DE = 4 (cm)
Suy ra: CE = CD – DE = 9 – 4 = 5 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông BCE ta có:
\(B{C^2} = B{E^2} + C{E^2}\)
Suy ra: \(B{E^2} = B{C^2} – C{E^2} = {13^2} – {5^2} = 144\)
BE = 12 (cm)
Vậy: AD = 12 (cm)
b) Gọi I là trung điểm của BC
Ta có: \(IB = IC = {1 \over 2}BC = {1 \over 2}.13 = 6,5 (cm)\) (1)
Kẻ IH ⊥ AD. Khi đó HI là đường trung bình của hình thang ABCD.
Advertisements (Quảng cáo)
Ta có: \(HI = {{AB + CD} \over 2} = {{4 + 9} \over 2} = 6,5\) (cm) (2)
Từ (1) và (2) suy ra: IB = HI = R
Vậy đường tròn \(\left( {I;{{BC} \over 2}} \right)\) tiếp xúc với đường thẳng AD.
Câu 40: Cho đường tròn (O), bán kính OA, dây CD là đường trung trực của OA.
a) Tứ giác OCAD là hình gì ? Vì sao?
b) Kẻ tiếp tuyến đường tròn tại C, tiếp tuyến này cắt đường thẳng OA tại I. Tính độ dài CI biết OA = R.
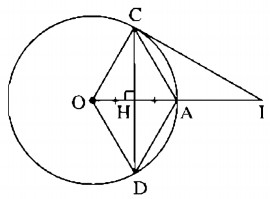
a) Gọi H là giao điểm của OA và CD
Vì CD là đường trung trực của OA nên:
CD ⊥ OA và HA = HO
Mà CD ⊥ OA nên HC = HD (đường kính dây cung)
Vì tứ giác ACOD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Đồng thời CD ⊥ OA nên ACOD là hình thoi.
b) Vì ACOD là hình thoi nên AC = OC
Mà OC = OA ( = R) nên tam giác OAC đều
Suy ra: \(\widehat {COA} = 60^\circ \) hay \(\widehat {COI} = 60^\circ \)
Mà CI ⊥ OC (tính chất tiếp tuyến)
Trong tam giác vuông OCI, ta có:
\(CI = OC.tg\widehat {COI} = R.tg60^\circ = R\sqrt 3 \).

