Câu 34*: Cho đường tròn (O) và hai điểm A, B nằm bên trong đường tròn và không cùng thuộc một đường kính. Dựng hai dây song song và bằng nhau sao cho điểm A nằm trên một dây, điểm B nằm trên dây còn lại.
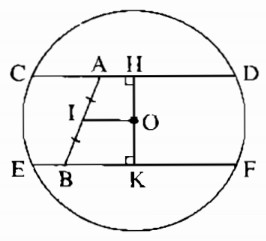
* Cách dựng
− Dựng trung điểm I của AB.
− Qua A dựng dây CD song song với OI.
− Qua B dựng dây EF song song với OI.
Ta được CD và EF là hai dây cần dựng.
* Chứng minh
Ta có: CD // OI, EF // OI
Suy ra: CD // EF
Kẻ OH ⊥ CD cắt EF tại K
Suy ra: OK ⊥ EF
Advertisements (Quảng cáo)
Lại có: IA = IB
Suy ra: OH = OK
Vậy CD = EF.
Câu 3.1: Cho đường tròn (O) đường kính 6cm, dây AB bằng 2cm. Khoảng cách từ O đến AB bằng
(A) \(\sqrt {35} cm\) ; (B) \(\sqrt 5 cm\) ;
(C) \(4\sqrt 2 cm\) ; (D) \(2\sqrt 2 cm\).
Hãy chọn phương án đúng.
Advertisements (Quảng cáo)
Chọn (D).
Câu 3.3*: Cho đường tròn (O ; 25cm), điểm C cách O là 7cm. Có bao nhiêu dây đi qua C có độ dài là một số nguyên xentimét?
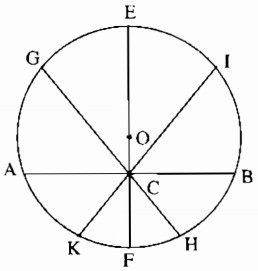
Dây lớn nhất đi qua C là đường kính EF = 50cm.
Dây nhỏ nhất đi qua C là dây AB vuông góc với
OC tại C, AB = 48cm.
Có hai dây đi qua C có độ dài 49cm ( là dây GH
và IK đối xứng nhau qua EF).
Có tất cả 4 dây đi qua C có độ dài là một số nguyên xentimét.
Câu 3.2: Cho đường tròn (O), điểm I nằm bên trong đường tròn ( I khác O). Dựng dây AB đi qua I và có độ dài ngắn nhất.
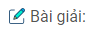
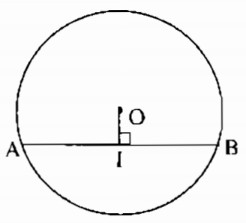
Dây AB phải dựng vuông góc với OI tại I.

