Câu 28: Tam giác ABC nội tiếp đường tròn (O) có \(\widehat A > \widehat B > \widehat C.\) Gọi OH, OI, OK theo thứ tự là khoảng cách từ O đến BC, AC, AB. So sánh các độ dài OH, OI, OK.
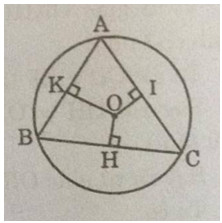
Tam giác ABC có \(\widehat A > \widehat B > \widehat C\) nên suy ra:
BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)
Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)
Mà BC < AC > AB nên suy ra:
OH < OI < OK ( dây lớn hơn gần tâm hơn).
Câu 29: Cho đường tròn (O), hai dây AB, CD bằng nhau và cắt nhau tại điểm I nằm bên trong đường tròn. Chứng minh rằng:
a) IO là tia phân giác của một trong hai góc tạo bởi hai dây AB và CD.
b) Điểm I chia AB, CD thành các đoạn thẳng bằng nhau đôi một.
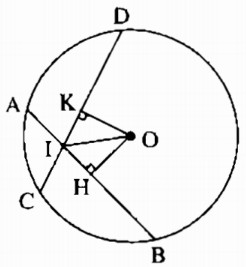
a) Kẻ OH ⊥ AB, OK ⊥ CD
Ta có: AB = CD (gt)
Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)
Advertisements (Quảng cáo)
Vậy OI là tia phân giác cảu góc BID (tính chất đường phân giác)
b) Xét hai tam giác OIH và OIK, ta có:
\(\widehat {OHI} = \widehat {OKI} = 90^\circ \)
OI chung
OH = OK (chứng minh trên)
Suy ra: ∆OIH = ∆OIK (cạnh huyền, cạnh góc vuông)
Suy ra: IH = IK (1)
Lại có: \(HA = HB = {1 \over 2}AB\)
\(KC = KD = {1 \over 2}CD\)
Mà AB = CD nên HA = KC (2)
Advertisements (Quảng cáo)
Từ (1) VÀ (2) suy ra: IA = IC
Mà A = CD nên IB = ID.
Câu 30: Cho đường tròn tâm O bán kính 25cm. Hai dây AB, CD song song với nhau và có độ dài theo thứ tự bằng 40cm, 48cm. Tính khoảng cách giữa hai dây ấy.
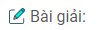
Kẻ \(OK \bot CD \Rightarrow CK = DK = {1 \over 2}CD\)
Kẻ \(OH \bot AB \Rightarrow AH = BH = {1 \over 2}AB\)
Vì AB // CD nên H, O, K thẳng hàng.
Áp dụng định lí Pi-ta-go vào tam giác vuông OBH, ta có:
\(O{B^2} = B{H^2} + O{H^2}\)
Suy ra: \(O{H^2} = O{B^2} – B{H^2} = {25^2} – {20^2} = 225\)
OH = 15 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ODK, ta có:
\(O{D^2} = D{K^2} + O{D^2}\)
Suy ra: \(O{K^2} = O{D^2} – D{K^2} = {25^2} – {24^2} = 49\)
OK = 7 (cm)
* Trường hợp O nằm giữa hai dây AB và CD (hình a):
HK = OH + OK = 15 + 7 =22 (cm)
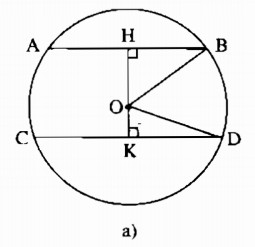
* Trường hợp O nằm ngoài hai dây AB và CD (hình b):
HK = OH – OK = 15 – 7 = 8 (cm).

