Câu 2.16: Cho tam giác ABC có \(\widehat A = 60^\circ \). Chứng minh rằng
BC2 = AB2 + AC2 – AB.AC.

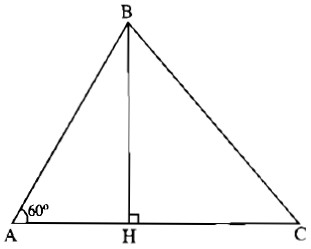
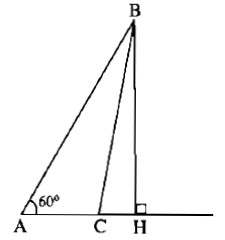
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để \(\widehat {BAC} = 60^\circ \) là góc nhọn ), do đó HC2 = (AC – AH)2
Công thức Py-ta-go cho ta:
BC2 = BH2 + HC2
= BH2 + (AC – AH)2
= BH2 + AH2 +AC2 – 2AC.AH
= AB2 + AC2 – 2AC.AH.
Do \(\widehat {BAC} = 60^\circ \) nên AH = AB cos60º = \({{AB} \over 2},\) suy ra BC2 = AB2 + AC2 − AB.AC .
Câu 2.17: Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo chứng minh rằng
Advertisements (Quảng cáo)
\({S_{ABCD}} = {1 \over 2}AC.BD.\sin a.\)

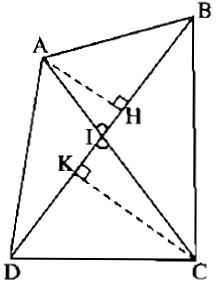
Giả sử hai đường chéo AC, BD cắt nhau tại I, \(\widehat {AIB} = \alpha \) là góc nhọn.
Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.
Ta có: AH = AIsinα, CK = CIsinα, diện tích tam giác ABD là \({S_{ABD}} = {1 \over 2}BD.AH,\) diện tích tam giác CBD là: \({S_{CBD}} = {1 \over 2}BD.CK.\)
Từ đó diện tích S của tứ giác ABCD là:
Advertisements (Quảng cáo)
\(\eqalign{
& S = {S_{ABD}} + {S_{CBD}} \cr
& = {1 \over 2}BD.(AH + CK) \cr
& = {1 \over 2}BD.(AI + CI)\sin \alpha \cr
& = {1 \over 2}{\rm{BC}}{\rm{.ACs}}in\alpha \cr} \)
Câu 2.18: Cho góc nhọn α
a) Chứng minh rằng \({{1 – tg\alpha } \over {1 + tg\alpha }} = {{\cos \alpha – \sin \alpha } \over {\cos \alpha + \sin \alpha }}.\)
b) Cho \(tg\alpha = {1 \over 3}.\) Tính \({{\cos \alpha – \sin \alpha } \over {\cos \alpha + \sin \alpha }}\).

a) \({{1 – tg\alpha } \over {1 + tg\alpha }} = {{1 – {{\sin \alpha } \over {\cos \alpha }}} \over {1 + {{\sin \alpha } \over {\cos \alpha }}}} = {{\cos \alpha – \sin \alpha } \over {\cos \alpha + \sin \alpha }}.\)
b) \({{\cos \alpha – \sin \alpha } \over {\cos \alpha + \sin \alpha }} = {{1 – tg\alpha } \over {1 + tg\alpha }} = {{1 – {1 \over 3}} \over {1 + {1 \over 3}}} = {1 \over 2}.\)
Câu 2.19: Tính giá trị của biểu thức
a) \({{3\cot g60^\circ } \over {2{{\cos }^2}30^\circ – 1}}\); b) \({{\cos 60^\circ } \over {1 + \sin 60^\circ }} + {1 \over {tg30^\circ }}.\)

a)
\(\eqalign{
& {{3\cot g60^\circ } \over {2{{\cos }^2}30^\circ – 1}} \cr
& = {{\sqrt 3 } \over {2{{\left( {{{\sqrt 3 } \over 2}} \right)}^2} – 1}} \cr
& = {{\sqrt 3 } \over {{3 \over 2} – 1}} = 2\sqrt 3 \cr} \)
b)
\(\eqalign{
& {{\cos 60^\circ } \over {1 + \sin 60^\circ }} + {1 \over {tg30^\circ }} \cr
& = {{{1 \over 2}} \over {1 + {{\sqrt 3 } \over 2}}} + \sqrt 3 \cr
& = {1 \over {2 + \sqrt 3 }} + \sqrt 3 \cr
& = {{2(2 + \sqrt {3)} } \over {2 + \sqrt 3 }} = 2. \cr} \)

