Bài 3. Góc nội tiếp – SBT Toán lớp 9: Giải bài 15, 16, 17 trang 102 Sách bài tập Toán 9 tập 2. Câu 15: Cho đường tròn tâm O, bán kính 1,5cm. Hãy vẽ hình vuông ABCD có bốn đỉnh nằm trên đường tròn đó. Nêu cách vẽ; Cho đường tròn (O) và hai dây AB, AC bằng nhau. Qua A vẽ một cát tuyến cắt dây BC ở D và cắt đường tròn (O) ở E. Chứng minh rằng
Câu 15: Cho đường tròn tâm O, bán kính 1,5cm. Hãy vẽ hình vuông ABCD có bốn đỉnh nằm trên đường tròn đó. Nêu cách vẽ.
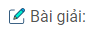
– Vẽ đường tròn (0; 1,5cm)
– Vẽ 2 đường kính AC và BD vuông góc với nhau.
– Nối AB, BC, CD, DA ta có tứ giác ABCD là hình vuông có 4 đỉnh nằm trên cung tròn (0; 1,5cm).
Thật vậy: OA = OC, OB = OD nên tứ giác ABCD là hình bình hành
Lại có: AC = BD và \(BD \bot AC\).
Vậy: tứ giác ABCD là hình vuông.
Câu 16: Cho đường tròn (O) và hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng \(\widehat {MSD} = 2\widehat {MBA}\).
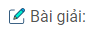
Advertisements (Quảng cáo)
\(SM \bot OM\) (tính chất tiếp tuyến)
\( \Rightarrow \Delta OMS\) vuông tại M
\(\widehat {MSO} + \widehat {MOS} = {90^0}\)
\(AB \bot CD\) (gt)
\( \Rightarrow \widehat {MOS} + \widehat {MOA} = {90^0}\)
Suy ra: \(\widehat {MSO} = \widehat {MOA}\) hay \(\widehat {MSD} = \widehat {MOA}\) (1)
Advertisements (Quảng cáo)
\(\widehat {MOA} = 2\widehat {MBA}\) (góc ở tâm và góc nội tiếp cùng chắn cung \(\overparen{AM}\)) (2)
Từ (1) và (2) suy ra: \(\widehat {MSD} = 2\widehat {MBA}\)
Câu 17: Cho đường tròn (O) và hai dây AB, AC bằng nhau. Qua A vẽ một cát tuyến cắt dây BC ở D và cắt đường tròn (O) ở E. Chứng minh rằng \(A{B^2} = AD.AE\).
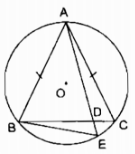
AB = AC (gt)
\(\overparen{AB}\) = \(\overparen{AC}\) (hai dây bằng nhau căng 2 cung bằng nhau)
\( \Rightarrow \widehat {ABC} = \widehat {AEB}\) (2 góc nội tiếp chắn 2 cung bằng nhau)
Xét ∆ABD và ∆ABE:
\(\widehat A\) chung
\(\widehat {ABC} = \widehat {AEB}\) (chứng minh trên)
Hay \(\widehat {ABD} = \widehat {AEB}\)
Suy ra: ∆ABD đồng dạng ∆AEB
\({{AE} \over {AB}} = {{AB} \over {AD}} \Rightarrow {\rm A}{{\rm B}^2} = AD.AE\).

