Câu 1: Cho hình chữ nhật ABCD có AD = 12cm, CD = 16cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

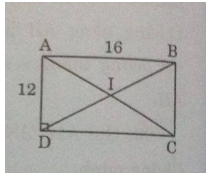
Gọi I là giao điểm của hai đường chéo AC và BD. Ta có:
IA = IB = IC = ID (tính chất hình chữ nhật)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn bán kính \({{AC} \over 2}\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC ta có:
\(\eqalign{
& A{C^2} = A{B^2} + B{C^2} = {16^2} + {12^2} \cr
& = 256 + 144 = 400 \cr} \)
Suy ra: \(AC = \sqrt {400} = 20\,(cm)\)
Vậy bán kính đường tròn là: \(IA = {{AC} \over 2} = {{20} \over 2} = 10\,(cm)\)
Câu 2: Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí tương đối của mỗi điểm: A( 1 ; -1), \(B( – \sqrt 2 ;\sqrt 2 )\) và C( 1 ; 2) đối với đường tròn (O ; 2 ).

Advertisements (Quảng cáo)
Gọi R là bán kính của đường tròn (O ; 2). Ta có R = 2
\(O{A^2} = {1^2} + {1^2} = 2 \Rightarrow OA = \sqrt 2 < 2\)
Vì OA < R nên điểm A nằm trong đường tròn (O; 2)
\(\eqalign{
& O{B^2} = {(\sqrt 2 )^2} + {(\sqrt 2 )^2} \cr
& = 2 + 2 = 4 \Rightarrow OB = 2 \cr} \)
Vì OB = R nên điểm B thuộc đường tròn (O; 2)
\(\eqalign{
& O{C^2} = {1^2} + {2^2} = 1 + 4 = 5 \cr
& \Rightarrow OC = \sqrt 5 > 2 \cr} \)
Vì OC > R nên điểm C nằm ngoài đường tròn (O; 2).
Câu 3: Hãy nối mỗi ô ở cột trái với mỗi ô ở cột phải để được khẳng định đúng
Advertisements (Quảng cáo)
|
(1)Tập hợp các điểm có khoảng cách đến điểm O cố định bằng 3cm |
(4) có khoảng cách đến điểm O nhỏ hơn hoặc bằng 3cm. |
|
(2)Đường tròn tâm O bán kính 3cm gồm tất cả những điểm |
(5) cách điểm O một khoảng bằng 3cm. |
|
(3) Hình tròn tâm O bán kình 3cm gồm tất cả những điểm |
(6) là đường tròn tâm O bán kính 3cm. |
|
|
(7) có khoảng cách đến điểm O lớn hơn 3cm. |

(1) nối với (6)
(2) nối với (5)
(3) nối với (4).
Câu 4: Cho góc nhọn xOy và hai điểm D, E thuộc tia Oy. Dựng đường tròn tâm M đi qua D và E sao cho tâm M nằm trên tia Ox.

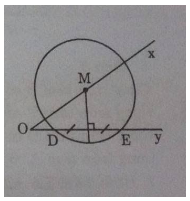
* Cách dựng
− Dựng đường trung trực của DE cắt Ax tại M.
− Dựng đường tròn tâm M bán kính MD.
* Chứng minh
Theo cách dựng ta có:
\(M \in Ox\)
MD = ME (tính chất đường trung trực)
Suy ra: \(E \in (M;MD)\)

