Câu 86: Cho hình sau trong đó G là trọng tâm của tam giác ABC. Chứng minh rằng:
a) \({S_{AGC}} = 2{{\rm{S}}_{GMC}}\)
b) \({S_{Gmb}} = {S_{GMC}}\)
c) \({S_{AGB}} = {S_{AGC}} = {S_{BGC}}\)
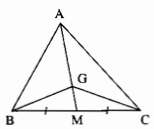
a) G là trọng tâm của ∆ABC
\( \Rightarrow \) GA = 2GM (tính chất đường trung tuyến)
∆AGC và ∆GMC có chung đường cao kẻ từ đỉnh C đến AM.
Cạnh đáy GA = 2GM
Chiều cao chung của hai tam giác
Suy ra: \({S_{AGC}} = 2{{\rm{S}}_{GMC}}\) (1)
b) ∆GMB và ∆GMC có cạnh đáy MB = MC, chung chiều cao kẻ từ đỉnh G đến cạnh BC
Advertisements (Quảng cáo)
\({S_{Gmb}} = {S_{GMC}}\) (2)
c) Hai tam giác AGB và GMB có chung chiều cao kẻ từ đỉnh B đến cạnh AM.
AG = 2GM (chứng minh trên)
Suy ra:
\(\eqalign{
& {S_{AGB}} = 2{{\rm{S}}_{GMB}}\left( 3 \right) \cr
& {S_{BGC}} = {S_{GMB}} + {S_{GMC}} = 2{S_{GMB}}\left( 4 \right) \cr} \)
Từ (1), (2) và (3) suy ra: \({{\rm{S}}_{AGC}} = {S_{AGB}} = {S_{BGC}}\)
Câu 87: Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy.
Advertisements (Quảng cáo)
a) Hãy tìm điểm M nằm trong góc xOy, cách đều Ox, Oy và cách đều A, B.
b) Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a?
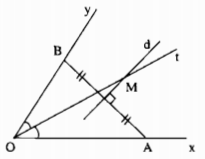
a) – Điểm nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên nó thuộc tia phân giác Ot của \(\widehat {xOy}\).
– Điểm cách đều 2 điểm A và B thuộc đường thẳng d là đường trung trực của AB
Vậy M là giao điểm của dường trung trực của đoạn thẳng AB và tia phân giác Ot của \(\widehat {xOy}\)
b) Nếu OA = OB
\( \Rightarrow \) ∆OAB cân tại O
Tia phân giác của \(\widehat {xOy}\) cũng là đường trung trực của AB. Vậy bất kỳ điểm M nào nằm trên tia phân giác của \(\widehat {xOy}\) đều thỏa mãn điều kiện câu a.
Câu 88: Cho góc xOy khác góc bẹt. Dùng một chiếc thước thẳng có chia khoảng, hãy nêu cách vẽ tia phân giác của góc xOy.
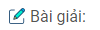
– Dùng thước chia khoảng, trên Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB.
– Nối AB
– Dùng thước chia khoảng, đo đoạn AB, lấy trung điểm M của AB.
– Kẻ tia OM.
Ta có ∆OAB cân tại O, OM là đường trung tuyến nên OM cũng là đường phân giác \(\widehat {AOB}\).
Vậy OM là tia phân giác của \(\widehat {xOy}\).

