Bài III.5: Để đẩy một con lăn nặng, bán kính R lên bậc thềm, người ta đặt vào nó một lực F theo phương ngang hướng đến trục (H.III.4). Lực này có độ lớn bằng trọng lượng của con lăn. Hãy xác định độ cao cực đại của bậc thềm.
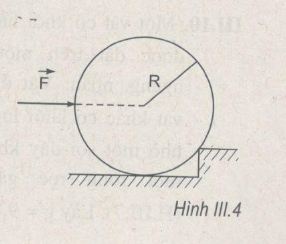
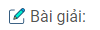
Con lăn vượt qua được bậc thềm nếu momen của lực \(\overrightarrow F \) đối với trục quay A lớn hơn hoặc bằng momen của trọng lực \(\overrightarrow P \) (H.III.4G)
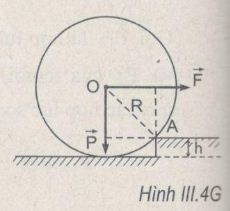
\(F(R – h) \ge P\sqrt {{R^2} – {{(R – h)}^2}} \)
\(F(R – {h_m}) \ge P\sqrt {{R^2} – {{(R – {h_m})}^2}} \)
\(2h_m^2 – 4R{h_m} + {R^2} = 0\)
Vì chỉ lấy nghiệm 0 < h < R nên ta được hmax = 0,29R
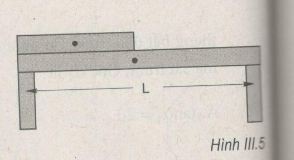
Bài III.6: Một thanh dầm bằng thép có khối lượng 1 000 kg. Trên thanh dầm này có một thanh dầm khác giống hệt nhưng có chiều dài bằng một nửa (H.III.5). Hỏi mỗi cột đỡ chịu một lực bằng bao nhiêu ? Lấy g = 10 m/s2.
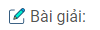
Advertisements (Quảng cáo)
Ta phân tích lực \(\overrightarrow {{P_1}} \) thành hai lực tác dụng lên hai cột
P11 = P12 = 0,5P1 = 0,5mg = 5000 N.
Làm tương tự với \(\overrightarrow {{P_2}} \) ta được
P21 + P22 = P2 = 0,5mg
\({{{P_{21}}} \over {{P_{22}}}} = {1 \over 3}\)
Suy ra \({P_{21}} = {{mg} \over 8} = {{10000} \over 8} = 1250(N)\)
\({P_{22}} = {{3mg} \over 8} = 3750(N)\)
Advertisements (Quảng cáo)
Áp lực lên cột 1 là: F1 = P11 + P21 = 6250 N.
Áp lực lên cột 2 là: F2 = P12 + P22 = 8750 N.
Bài III.7: Người ta khoét một lỗ tròn bán kính R/2 trong một đĩa phẳng mỏng, đồng chất, bán kính R (H.III.6). Tìm trọng tâm của phần còn lại.
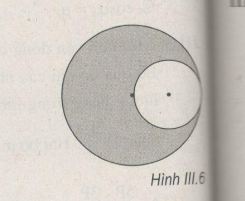
Giả sử ta khoét thêm một lỗ tròn bán kính R/2 nữa đối xứng với lỗ tròn đã khoét lúc đầu (H.III.6G)
Gọi \(\overrightarrow {{P}} \) là trọng lượng của đĩa bán kính R khi chưa bị khoét, \(\overrightarrow {{P_1}} \) là trọng lượng của đĩa nhỏ có bán kính R/2 và \(\overrightarrow {{P_2}} \) là trọng lượng của phần đĩa còn lại sau hai lần khoét, ta có:
\({{{P_1}} \over P} = {{{S_1}} \over S} = {{{{\pi {R^2}} \over 4}} \over {\pi {R^2}}} = {1 \over 4}\) ; \({{{P_2}} \over P} = {{S – 2{S_1}} \over S} = {{S – {S \over 2}} \over S} = {1 \over 2}\)
=> \({{{P_1}} \over {{P_2}}} = {1 \over 2}\)
Do tính chất đối xứng, trọng tâm phần đĩa còn lại sau hai lần khoét thì trùng với tâm O của đĩa khi chưa khoét, còn trọng tâm của đĩa nhỏ mà ta giả sử khoét thêm thì ở tâm O1 của nó. Gọi G là trọng tâm của đĩa sau khi bị khoét một lỗ tròn. Ta có hệ phương trình
\(\left\{ \matrix{
{{GO} \over {G{O_1}}} = {{{P_1}} \over {{P_2}}} = {1 \over 2} \hfill \cr
GO + G{O_1} = {R \over 2} \hfill \cr} \right.\)
Giải ra ta được: \(G{O_1} = {R \over 3}\) và \(GO = {R \over 6}\)
Bài III.8: Lực của gió tác dụng vào cánh buồm của một chiếc thuyền buồm là F1 = 380 N hướng về phía Bắc. Nước tác dụng vào thuyền một lực F2 = 190 N hướng về phía Đông. Thuyền có khối lượng tổng cộng là 270 kg. Hỏi độ lớn và hướng của gia tốc của thuyền ?
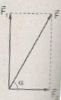
Từ hình vẽ, ta có
\(F = \sqrt {F_1^2 + F_2^2} = \sqrt {{{380}^2} + {{190}^2}} = > F \approx 425N\)
\(\tan \alpha = {{{F_1}} \over {{F_2}}} = 2 = > \alpha = 63,{5^0}\)
\(a = {F \over m} = {{425} \over {270}} = 1,57(m/{s^2})\) , theo hướng Đông – Bắc.

