Câu 82: Tính cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 13cm, cạnh góc vuông kia bằng 12cm.
Giả sử ∆ABC có \(\widehat A = 90^\circ \), BC = 13cm, AC = 12cm
Theo định lý Pytago, ta có: \(B{C^2} = A{B^2} + A{C^2}\)
Suy ra: \({\rm{A}}{B^2} = B{C^2} – A{C^2} = {13^2} – {12^2} = {25^2}\)
Vậy AB = 5 (cm)
Câu 83: Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AC = 20cm, AH = 12cm, BH = 5cm
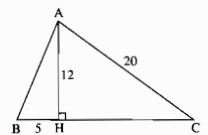
∆AHB có \(\widehat {AHB} = 90^\circ \)
Theo định lý Pytago, ta có:
Advertisements (Quảng cáo)
\(\eqalign{
& A{B^2} = A{H^2} + H{B^2} \cr
& \Rightarrow A{B^2} = {12^2} + {5^2} = 169 \cr} \)
Vậy AB = 13 (cm)
∆AHC có \(\widehat {AHC} = 90^\circ \)
Theo định lý Pytago, ta có:
\(\eqalign{
& A{C^2} = A{H^2} + H{C^2} \cr
& \Rightarrow H{C^2} = A{C^2} – A{H^2} = {20^2} – {12^2} = 400 – 144 = 256 \cr} \)
Vậy HC = 16(cm)
Advertisements (Quảng cáo)
Ta có: BC = BH + HC = 5 + 16 = 21 (cm)
Chu vi tam giác ABC là:
AB + AC + BC = 13 + 20 + 21 = 54 (cm)
Câu 84: Tính độ dài các đoạn thẳng AB, BC, CD, DA trên hình dưới.
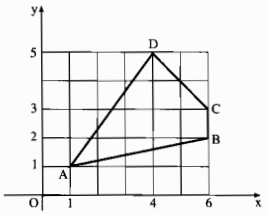
Theo định lý Pytago, ta có:
\(\eqalign{
& A{B^2} = {5^2} + {1^2} = 25 + 1 = 26 \Rightarrow AB = \sqrt {26} \cr
& C{{\rm{D}}^2} = {2^2} + {2^2} = 4 + 4 = 8 \Rightarrow C{\rm{D}} = \sqrt 8 \cr
& A{{\rm{D}}^2} = {3^2} + {4^2} = 9 + 16 = 25 \Rightarrow A{\rm{D}} = 5 \cr} \)
Và BC = 1
Câu 85: Màn hình của một máy thu hình có dạng hình chữ nhật, chiều rộng 12 inh-sơ, đường chéo 20 inh-sơ. Tính chiều dài.
Giả sử màn hình máy thu hình là hình chữ nhật ABCD, chiều rộng BC = AD, chiều dài AB = CD , đường chéo AC = BD.
Ta có tam giác ABD vuông tại A
Theo định lý Pytago, ta có: \(B{{\rm{D}}^2} = A{B^2} + A{{\rm{D}}^2}\)
\( \Rightarrow A{B^2} = B{{\rm{D}}^2} – A{{\rm{D}}^2} = {20^2} – {12^2} = 400 – 144 = 256\)
Vậy AB = 16 (inh-sơ)

