Câu 86: Tính đường chéo của một mặt bàn hình chữ nhật có chiều dài 10dm, chiều rộng 5dm.
Giả sử mặt bàn là hình chữ nhật ABCD, chiều rộng BC = AD, chiều dài AB = CD, đường chéo AC = BD.
Ta có tam giác ABD vuông tại A
Theo định lí Pytago, ta có: \(B{{\rm{D}}^2}{\rm{ = A}}{{\rm{B}}^2}{\rm{ + A}}{{\rm{D}}^2}\)
\(B{{\rm{D}}^2} = {10^2} + {5^2} = 100 + 25 = 125\)
Vậy \(BD = \sqrt {125} \approx 11,2\left( {dm} \right)\)
Câu 87: Hai đoạn thẳng AC, BD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đoạn thẳng. Tính các độ dài AB, BC, CD, DA biết AC = 12cm, BD = 16cm.
Advertisements (Quảng cáo)
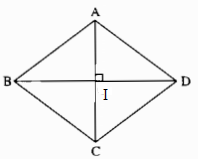
Gọi I là giao điểm của AC và BD.
Ta có:
\(\eqalign{
& IA = IC = {{AC} \over 2} = 6(cm) \cr
& IB = I{\rm{D}} = {{B{\rm{D}}} \over 2} = 8\left( {cm} \right) \cr} \)
Áp dụng định lý Pytago vào tam giác vuông AIB, ta có:
Advertisements (Quảng cáo)
\(\eqalign{
& A{B^2} = I{A^2} + I{B^2} \cr
& A{B^2} = {6^2} + {8^2} = 36 + 64 = 100 \cr} \)
Vậy AB = 10 (cm)
Mặt khác: ∆IAB = ∆IAD = ∆ICB = ∆ICD (c.g.c)
Suy ra: AD = BC = CD = AB = 10 (cm)
Câu 88: Tính độ dài các cạnh góc vuông của một tam giác vuông cân có cạnh huyền bằng:
a) 2cm
b) \(\sqrt 2 cm\)
Tam giác vuông cân là tam giác vuông có 2 cạnh góc vuông bằng nhau. Gọi độ dài cạnh góc vuông là x (cm) (x > 0)
a) Áp dụng định lý Pytago ta có:
\({{\rm{x}}^2} + {x^2} = {2^2} \Rightarrow 2{{\rm{x}}^2} = 4 \Rightarrow {x^2} = 2 \Rightarrow x = \sqrt 2 \)
b) Áp dụng định lý Pytago, ta có:
\(\eqalign{
& {{\rm{x}}^2} + {x^2} = {\left( {\sqrt 2 } \right)^2} \cr
& 2{{\rm{x}}^2} = 2 \Rightarrow {x^2} = 1 \Rightarrow x = 1\left( {cm} \right) \cr} \)

