Câu 79: Cho đường tròn tâm O đường kính AB. Gọi M là một điểm nằm trên đường tròn, tính số đo góc AMB.
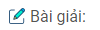
Nối OM, ta có:
OA = OM (bán kính đường tròn tâm O)
Nên ∆OAM cân tại O
\( \Rightarrow \widehat A = \widehat {{M_1}}\) (tính chất tam giác cân)
OM = OB (bán kính đường tròn tâm O)
Suy ra: ∆OAM cân tại O
\( \Rightarrow \widehat {{M_2}} = \widehat B\) (tính chất tam giác cân)
Trong ∆AMB, ta có:
\(\widehat A + \widehat {AMB} + \widehat B = 180^\circ \) (tổng 3 góc trong tam giác)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat A + \widehat {{M_1}} + \widehat {{M_2}} + \widehat B = 180^\circ \) (3)
Từ (1), (2) và (3) suy ra: 2\(\left( {\widehat {{M_1}} + \widehat {{M_2}}} \right) = 180^\circ \)
Vậy \(\widehat {{M_1}} + \widehat {{M_2}} = 90^\circ \) hay \(\widehat {AMB} = 90^\circ \)
Câu 80: Đặt đề toán theo hình dưới. Sau đó vẽ lại hình theo đề toán rồi đo góc DAE.
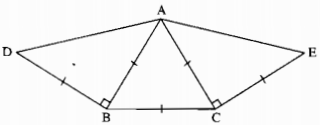
Đề toán:
Advertisements (Quảng cáo)
– Vẽ ∆ABC đều.
– Vẽ ∆ABD vuông cân tại B sao cho D và C nằm trên hai nửa mặt phẳng đối có bờ chứa đường thẳng AB.
– Vẽ ∆ACE vuông cân tại C sao cho E và B nằm trên hai nửa mặt phẳng đối bờ có chứa đường thẳng AC.
Đo \(\widehat {DA{\rm{E}}} = 150^\circ \)
*Chứng minh:
\(\widehat {DA{\rm{E}}} = \widehat {DAB} + \widehat {BAC} + \widehat {CA{\rm{E}}} = 45^\circ + 60^\circ + 45^\circ = 150^\circ \)
Câu 81: Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình 62) là tam giác nhọn.
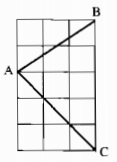
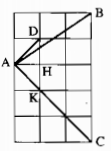
Nối A với điểm D tạo thành đường chéo ô vuông
Gọi K giao điểm AC với đỉnh ô vuông, H là giao điểm DK với đường kẻ ô vuông từ A.
Ta có: ∆AHK vuông cân tại H => \(\widehat {HAK} = 45^\circ \)
∆AHD vuông cân tại H => \(\widehat {HA{\rm{D}}} = 45^\circ \)
\( \Rightarrow \widehat {DAK} = \widehat {HA{\rm{D}}} + \widehat {HAK} = 45^\circ + 45^\circ = 90^\circ \) hay \(\widehat {DAC} = 90^\circ \)
\( \Rightarrow \widehat {BAC} < 90^\circ \)
Trên hình vẽ: \(\widehat {ACB} < 90^\circ \) và \(\widehat {ABC} < 90^\circ \)
Vậy ∆ABC là tam giác nhọn.

