Câu 49
Vẽ tam giác ABC biết \(\widehat B = 90^\circ ,BC = 2cm,\widehat C = 60^\circ \). Sau đó đo AC để kiểm tra rằng AC = 4cm.
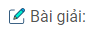
AC = 4cm.
Câu 50
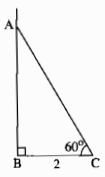
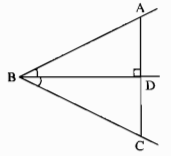
Tìm các tam giác bằng nhau ở hình dưới (không xét tam giác mà các cạnh chưa được kẻ)
Ta có: ∆ABD = ∆ CBD (g.c.g)
∆GIF = ∆HIE (g.c.g)
Câu 51: Cho tam giác ADE có \(\widehat D = \widehat E\). Tia phân giác của góc D cắt AE ở điểm M. Tia phân giác của góc E cắt AD ở điểm N. So sánh các độ dài DN và EM.
Advertisements (Quảng cáo)
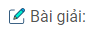
Tam giác ADE có: \(\widehat D = \widehat E\) (gt)
\(\widehat {{D_1}} = \widehat {{D_2}} = {1 \over 2}\widehat D\) (Vì DM là tia phân giác)
\(\widehat {{E_1}} = \widehat {{E_2}} = {1 \over 2}\widehat E\) (Vì EN là tia phân giác)
Suy ra: \(\widehat {{D_1}} = \widehat {{D_2}} = \widehat {{E_1}} = \widehat {{E_2}}\)
Xét ∆DNE = ∆EMD, ta có:
\(\widehat {N{\rm{D}}E} = \widehat {ME{\rm{D}}}\left( {gt} \right)\)
Advertisements (Quảng cáo)
DE cạnh chung
\(\widehat {{D_2}} = \widehat {{E_2}}\) (chứng minh trên)
Suy ra: ∆DNE = ∆EMD (g.c.g)
Vậy DE = EM (2 cạnh tương ứng).
Câu 52: Cho hình bên, trong đó AB // HK, AH // BK. Chứng minh rằng AB = HK, AH = BK.
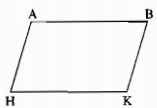
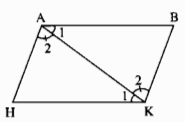
Nối AK. Ta có:
AB // HK (gt)
\( \Rightarrow \widehat {{A_1}} = \widehat {{K_1}}\) (hai góc so le trong)
AH // BK (gt)
\( \Rightarrow \widehat {{A_2}} = \widehat {{K_2}}\) (hai góc so le trong)
Xét ∆ABK và ∆KHA, ta có:
\(\widehat {{A_1}} = \widehat {{K_1}}\) (chứng minh trên)
AK cạnh chung
\(\widehat {{A_2}} = \widehat {{K_2}}\) (chứng minh trên)
Suy ra: ∆ABK = ∆KHA (g.c.g)
Vậy AB = KH, BK = AH (2 cạnh tương ứng)

