Câu 43: Cho tam giác ABC có \(\widehat A = 90^\circ \), trên cạnh BC lấy điểm E sao cho BE = BA. Tia phân giác của góc B cắt AC ở D.
a) So sánh các độ dài DA và DE.
b) Tính số đo góc BED.
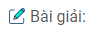
a) Xét ∆ABD và ∆EBD, ta có:
AB = BE (gt)
\(\widehat {AB{\rm{D}}} = \widehat {DBE}\) (vì BD là tia phân giác)
BC cạnh chung
Suy ra: ∆ABD = ∆EBD (c.g.c)
\( \Rightarrow \) DA = DE (2 cạnh tương ứng)
b) Ta có: ∆ABD = ∆EBD (chứng minh trên)
Suy ra: \(\widehat A = \widehat {BE{\rm{D}}}\) (2 góc tương ứng)
Mà \(\widehat A = 90^\circ \) nên \(\widehat {BE{\rm{D}}} = 90^\circ \).
Advertisements (Quảng cáo)
Câu 44: Cho tam giác AOB có AO = OB. Tia phân giác của góc O cắt AB ở D. Chứng minh rằng:
a) DA = DB
b) \(O{\rm{D}} \bot AB\)
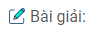
a) Xét ∆AOD và ∆BOD, ta có:
OA = OB (gt)
\(\widehat {AO{\rm{D}}} = \widehat {BO{\rm{D}}}\) (vì OD là tia phân giác)
Advertisements (Quảng cáo)
OD cạnh chung
Suy ra: ∆AOD = ∆BOD (c.g.c)
Vậy DA = DB (2 cạnh tương ứng)
b) ∆AOD = ∆BOD (chứng minh trên)
\( \Rightarrow \widehat {{D_1}} = \widehat {{D_2}}\) (2 góc tương ứng)
Ta có: \(\widehat {{D_1}} + \widehat {{D_2}} = 180^\circ\) (hai góc kề bù)
Suy ra: \(\widehat {{D_1}} = \widehat {{D_2}} = 90^\circ \)
Vậy \(O{\rm{D}} \bot AB\).
Câu 45: Cho các đoạn thẳng AB và CD trên giấy kẻ ô vuông (hình dưới). Chứng minh rằng AB = CD, AB // CD.
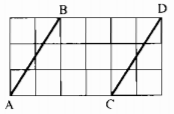
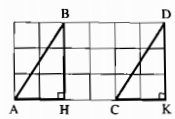
Gọi giao điểm của đường kẻ ô vuông đi qua điểm A và đi qua điểm B cắt nhau tại H ; đi qua điểm C và đi qua điểm D là K.
Xét ∆ AHB và ∆CKD, ta có:
AH = CK (gt)
\(\widehat {AHB} = \widehat {CK{\rm{D}}} = 90^\circ \)
BH = DK (bằng 3 ô vuông)
Suy ra: ∆ AHB = ∆CKD (c. g.c)
\( \Rightarrow \) AB = CD và \(\widehat {BAH} = \widehat {DCK}\)
Hai đường thẳng AB và CD cắt đường thẳng AK có 2 góc \(\widehat {BAH}\) và \(\widehat {DCK}\) ở vị trí đồng vị bằng nhau nên AB // CD.

