Câu 40: Qua trung điểm M của đoạn thẳng AB, kẻ đường thẳng vuông góc với AB. Trên đường thẳng đó lấy điểm K. Chứng minh rằng KM là tia phân giác của góc AKB.
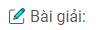
Xét ∆AMK và ∆BMK, ta có:
AM = BM (gt)
\(\widehat {AMK} = \widehat {BMK} = 90^\circ \) (vì \(KM \bot AB\))
MK cạnh chung
Suy ra: ∆AMK = ∆BMK(c.g.c)
\(\Rightarrow \widehat {AKM} = \widehat {BKM}\)
Vậy KM là tia phân giác của \(\widehat {AKB}\).
Advertisements (Quảng cáo)
Câu 41: Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng. Chứng minh rằng AC // BD.
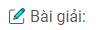
Xét ∆AOC và ∆BOD, ta có:
OA = OB (gt)
Advertisements (Quảng cáo)
\(\widehat {AOC} = \widehat {BO{\rm{D}}}\) (đối đỉnh)
OC = OD (gt)
Suy ra:∆AOC = ∆BOD (c.g.c)
\( \Rightarrow \widehat A = \widehat B\) (hai góc tương ứng)
Vậy: AC // BD (vì có hai góc ở vị trí so le trong bằng nhau)
Câu 42: Cho tam giác ABC có \(\widehat A = 90^\circ \). Trên tia đối của tia CA lấy điểm D sao cho CD = CA, Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Tính số đo góc CDE.
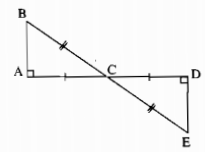
Xét ∆ABC và ∆DEC, ta có:
AC = DC (gt)
\(\widehat {ACB} = \widehat {EC{\rm{D}}}\) (đối đỉnh)
BC = EC (gt)
Suy ra: ∆ABC = ∆DEC (c.g.c)
\(\widehat A = \widehat D\) (hai góc tương ứng) mà \(\widehat A = 90^\circ \) nên \(\widehat D = 90^\circ \).

