Câu 23: Cho ∆ABC = ∆ DEF. Biết \(\widehat A = 55^\circ ;\widehat E = 75^\circ \). Tính các góc còn lại của mỗi tam giác.
Vì ∆ABC = ∆DEF nên: \(\widehat A = \widehat D;\widehat B = \widehat E;\widehat C = \widehat F\)
Mà: \(\widehat A = 55^\circ ,\widehat E = 75^\circ \) suy ra \(\widehat D = 55^\circ ,\widehat B = 75^\circ \)
Trong ∆ABC, ta có: \(\widehat {{A}} + \widehat {{B}} + \widehat {{C}} = 180^\circ \) (tổng ba góc trong tam giác)
Suy ra \(\widehat C = 180^\circ – \left( {\widehat A + \widehat B} \right) = 180^\circ – \left( {55^\circ + 75^\circ } \right) = 50^\circ \)
Vậy: \(\widehat F = 50^\circ \)
Câu 24: Cho hai tam giác bằng nhau: tam giác ABC và một tam giác có ba đỉnh là D, E, F. Hãy viết kí hiệu sự bằng nhau của hai tam giác đó, biết rằng:
a) \(\widehat A = \widehat F,\widehat B = \widehat E\)
b) \(AB = E{\rm{D}},AC = F{\rm{D}}\)
Advertisements (Quảng cáo)
a) Vì \(\widehat A = \widehat F\) nên đỉnh A tương ứng với đỉnh F
Vì \(\widehat B = \widehat E\) nên đỉnh B tương ứng với đỉnh E
Suy ra đỉnh C tương ứng với đỉnh D.
Vậy ∆ABC = ∆ FED
b) Ta có AB = ED và AC = FD nên đỉnh A tương ứng với đỉnh D, đỉnh B tương ứng đỉnh E, đỉnh C tương ứng đỉnh F.
Advertisements (Quảng cáo)
Vậy ∆ABC = ∆DEF.
Câu 25: Trên hình bên có một số tam giác bằng nhau. Hãy quan sát rồi phát hiện các tam giác bằng nhau trong hình vẽ (không xét các tam giác mà các cạnh chưa được kẻ) sau đó kiểm tra lại bằng cách đo.
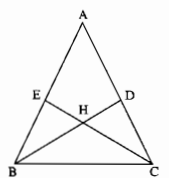
Có ba cặp tam giác bằng nhau:
∆ABD = ∆ ACE
∆BEC = ∆ CDB
∆BEH = ∆CDH
Câu 26: Cắt tam giác ABC bằng giấy có AB = AC và gấp hình theo tia phân giác của góc A. Nếu gấp chia tam giác ABC thành hai tam giác. Hãy đo để kiểm tra xem hai tam giác đó có bằng nhau hay không.
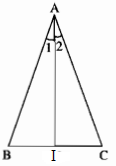
Gọi giao điểm của tia phân giác \(\widehat A\) với cạnh BC là I
Ta có: ∆ABI = ∆ACI
Ta có: ∆ABI = ∆ACI

