Câu 27: Vẽ đường thẳng a và điểm A không thuộc a. Vẽ đường thẳng b đi qua A và song song với a. Vẽ được mấy đường thẳng b như thế?
\(A \notin a;A \in b\)
Hình vẽ:
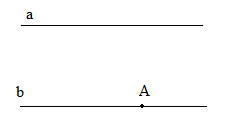
Theo tiên đề Ơclít, chỉ vẽ được một đường thẳng b.
Câu 28: Hãy điền vào chỗ trống (…) trong các phát biểu sau:
a) Qua điểm A ở ngoài đường thẳng a, có không quá một đường thẳng song song với…
b) Qua điểm A ở ngoài đường thẳng a, có nhiều nhất một đường thẳng song song với…
c) Qua điểm A ở ngoài đường thẳng a, chỉ có một đường thẳng song song với …
d) Nếu qua điểm A ở ngoài đường thẳng a, có hai đường thẳng song song với a thì….
e) Cho điểm A ở ngoài đường thẳng a. Đường thẳng đi qua A và song song với a là …
a) Qua điểm A ở ngoài đường thẳng a, có không quá một đường thẳng song song với đường thẳng a.
Advertisements (Quảng cáo)
b) Qua điểm A ở ngoài đường thẳng a, có nhiều nhất một đường thẳng song song với đường thẳng a.
c) Qua điểm A ở ngoài đường thẳng a, chỉ có một đường thẳng song song với đường thẳng a.
d) Nếu qua điểm A ở ngoài đường thẳng a, có hai đường thẳng song song với a thì chúng trùng nhau.
e) Cho điểm A ở ngoài đường thẳng a. Đường thẳng đi qua A và song song với a là duy nhất.
Câu 29: Vẽ hai đường thẳng a, b sao cho a // b. Vẽ đường thẳng c cắt a tại điểm A. Hỏi c có cắt b hay không?
a) Hãy vẽ hình, quan sát và trả lời câu hỏi trên.
b) Hãy suy ra rằng: Nếu a // b và c cắt a thì c cắt b.
Advertisements (Quảng cáo)
a) Hình vẽ:
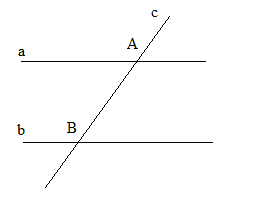
Ta có: a //b và c cắt a tại c thì c cắt b.
b) Ta có a //b, c cắt a tại A
Giả sử c không cắt b thì suy ra c //b. Vậy qua điểm A kẻ được 2 đường thẳng a và c cùng song song với b trái với tiên đề Ơclít
Vậy nếu a // b, c cắt a thì c cắt b.
Câu 30: Trên hình dưới, hai đường thẳng a, b song song với nhau, đường thẳng c cắt a tại A, cắt b tại B.
a) Lấy một cặp góc so le trong (chẳng hạn cặp \({{\rm{A}}_4},{B_1}\) rồi đo xem hai góc đó có bằng nhau hay không?
b) Hãy lí luận vì sao \(\widehat {{A_4}} = \widehat {{B_1}}\) theo gợi ý sau:
Nếu \(\widehat {{{\rm{A}}_4}} \ne \widehat {{B_1}}\) thì qua A ta vẽ tia Ap sao cho \(\widehat {PAB} = \widehat {{B_1}}\).
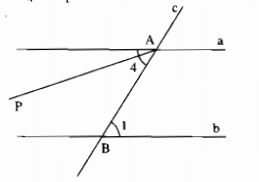
– Thế thì AP // b, vì sao?
– Qua A, vừa có a // b, vừa có AP // b, thì sao?
– Kết luận: Đường thẳng AP và đường thẳng a chỉ là một. Nói cách khác, \(\widehat {PAB} = \widehat {{A_4}}\), từ đó \(\widehat {{A_4}} = \widehat {{B_1}}\).
a) Có
b) Nếu \(\widehat {{A_4}} \ne \widehat {{B_1}}\), thì qua A ta vẽ tia AP sao cho \(\widehat {PAB} = \widehat {{B_1}}\)
Vì AP và b có cặp góc so le trong bằng nhau này nên AP // b
Khi đó, qua A ta vừa có a // b, vừa có AP // b, trái với tiên đề Ơclít về đường thẳng song song.
Vậy đường thẳng AP và đường thẳng a chỉ là một, hay \(\widehat {PAB} = \widehat {{A_4}}\) nghĩa là \(\widehat {{A_4}} = \widehat {{B_1}}\).

