Giải bài 1 trang 28 SBT Toán 6

Gọi P là tập hợp các số nguyên tố. Điền kí hiệu \( \in , \notin \)thích hợp vào chỗ chấm.
41 … P;
57 … P;
83 … P;
95 … P.
Cách 1: Tra các số trong bảng số nguyên tố (nhỏ hơn 1000) trang 47 SGK Toán 6 – Chân trời sáng tạo
Cách 2:
Bước 1: Phân tích số đó ra thừa số nguyên tố.
Bước 2: Suy ra các ước của số đó. Kết luận là số nguyên tố ( tức là \( \in \)P) hay hợp số (\( \notin \)P)

41 \( \in \)P;
57 \( \notin \)P (vì 57 \( \vdots \)3 nên không là số nguyên tố).
83 \( \in \)P;
95 \( \notin \)P (vì 95 \( \vdots \)5 nên không là số nguyên tố).
Bài 2 trang 28 SBT Toán 6

Dùng bảng nguyên tố tìm các số nguyên tố trong các số sau:
117;
131;
313;
469;
647
Các số nguyên tố là: 131; 313; 647.
Giải bài 3

Thay chữ số thích hợp vào dấu * để được mỗi số sau là:
a) hợp số: \(\overline {2*} ;\overline {3*} \)
b) số nguyên tố: \(\overline {1*} ;\overline {4*} \)

a) hợp số: 20; 21; 22; 24; 25; 26; 27; 28; 30; 32; 33; 34; 35; 36; 38; 39
b) số nguyên tố: 11; 13; 17; 19; 41; 43; 47.
Giải bài 4 trang 28 SBT Toán 6 CTST

Advertisements (Quảng cáo)
a) Điền “Đ” (đúng), “S”(sai) vào các ô trống cho mỗi kết luận trong bảng sau:
|
Kết luận |
Đ/S |
|
i. Mỗi số chẵn lớn hơn 2 đều là hợp số. |
|
|
ii. Tổng của hai số nguyên tố lớn hơn 2 luôn là một hợp số |
|
|
iii. Tổng của hai hợp số luôn là một hợp số. |
|
|
iv. Tích của hai số nguyên tố có thể là một số chẵn |
|
b) Với mỗi kết luận sai trong câu a, hãy cho ví dụ minh hoạ.

a)
|
Kết luận |
Đ/S |
|
i. Mỗi số chẵn lớn hơn 2 đều là hợp số. |
Đ |
|
ii. Tổng của hai số nguyên tố lớn hơn 2 luôn là một hợp số |
Đ |
|
iii. Tổng của hai hợp số luôn là một hợp số. |
S |
|
iv. Tích của hai số nguyên tố có thể là một số chẵn |
Đ |
b) Ví dụ: 14 và 9 là hai hợp số nhưng tổng 14 + 9 = 23 là số nguyên tố.
Bài 5 trang 29 SBT Toán 6

a) Viết mỗi số sau thành tổng của hai số nguyên tố:
16; 18; 20.
b) Viết 15 thành tổng của 3 số nguyên tố.

a) 16 = 5 + 11 = 3 + 13;
18 = 5 + 13 = 7 + 11 ;
20 = 3 + 17 = 7 + 13
b) 15 = 3 + 5 + 7
Giải bài 6 trang 29 Sbt Toán 6 tập 1
Phân tích các số sau ra thừa số nguyên tố bằng hai cách “theo cột dọc” và dùng “sơ đồ cây”:
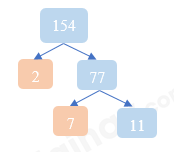
a) 154;
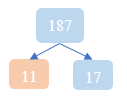
b) 187;
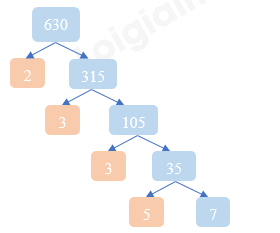
c) 630.

Advertisements (Quảng cáo)
a)
|
154 |
2 |
|
77 |
7 |
|
11 |
11 |
|
1 |
|
b)
|
187 |
11 |
|
17 |
17 |
|
1 |
|
c)
|
630 |
2 |
|
315 |
3 |
|
105 |
3 |
|
35 |
5 |
|
7 |
7 |
|
1 |
|
Giải bài 7 trang 29 SBT Toán lớp 6

Phân tích các số sau ra thừa số nguyên tố rồi tìm tập hợp các ước của mỗi số đó:
a) 38;
b) 75;
c) 100.

a) 38 = 2. 19
Tập hợp các ước của 38 là: {1; 2; 19; 38}.
b)
Tập hợp các ước của 75 là: {1; 3; 5; 15; 25; 75}.
c) \(100 = 2.2.5.5 = {2^2}{.5^2}\)
Tập hợp các ước của 100 là: {1; 2; 4; 5; 10; 20; 25; 50; 100}.
Giải bài 8 trang 29 Sách bài tập Toán 6 Chân trời sáng tạo

Bác Tâm xếp 360 quả trứng vào các khay đựng như Hình 1 và Hình 2 để mang ra chợ bán. Nếu chỉ dùng một loại khay đựng để xếp thì trong mỗi trường hợp, bác Tâm cần bao nhiêu khay để đựng hết số trứng trên?

Quan sát hình 1, dễ thấy: Khay có 3 hàng, mỗi hàng có 6 quả trứng.
Do đó mỗi khay ở Hình 1 đựng được số trứng là: 3.6=18 (quả)
Cần số khay để đựng 360 quả trứng là: 360 : 18 = 20 (khay)
Quan sát hình 2, dễ thấy: Khay có 5 hàng, mỗi hàng có 6 quả trứng.
Do đó mỗi khay ở Hình 1 đựng được số trứng là: 5.6=30 (quả)
Cần số khay để đựng 360 quả trứng là: 360 : 30 = 12 (khay)
Bài 9 trang 29 SBT Toán 6 tập 1 CTST

Tìm số nguyên tố p sao cho p +1 và p + 5 đều là số nguyên tố
Nhận xét về tính chẵn lẻ của p +1 và p + 5 khi p chẵn hoặc lẻ, từ đó suy ra giá trị p cần tìm.

Trường hợp 1: p chẵn
Do p là số nguyên tố nên p = 2, suy ra p +1 =3 và p + 5 = 7 đều là các số nguyên tố.
Vậy p = 2 thỏa mãn.
Trường hợp 2: p lẻ, do p là số nguyên tố nên p > 2
Khi đó p +1 và p + 5 đều là các số chẵn lớn hơn 2, vì vậy p + 1 và p + 5 là hợp số.
Vậy p = 2.
Giải bài 10 trang 29 SBT Toán lớp 6

a) Tìm số tự nhiên k để 3.k là số nguyên tố.
b) Tìm số tự nhiên k để 7.k là số nguyên tố.

a)
Nếu k = 0 thì 3k = 0, không là số nguyên tố
Nếu k >1, ta có 3.k chia hết cho 3 và k, do đó nó có ít nhất 3 ước là 1; 3; 3.k nên không là số nguyên tố.
Vậy k = 1.
b)
Nếu k = 0 thì 7k = 0, không là số nguyên tố
Nếu k >1, ta có 7.k chia hết cho 7 và k, do đó nó có ít nhất 3 ước là 1; 7; 7.k nên không là số nguyên tố.
Vậy k = 1.