Câu 37: Bạn Minh đã tìm ra 1 cách: “rút gọn” phân số rất đơn giản. Này nhé:
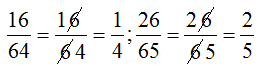
(“Rút gọn” cho 6)
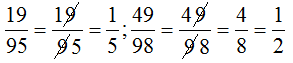
(“Rút gọn” cho 9)
Em hãy kiểm tra xem các kết quả tìm được có đúng không?
Em có thể áp dụng “phương pháp” này để rút gọn các phân số có dạng \({{\overline {ab} } \over {\overline {bc} }}\) hay không?
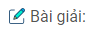
Các kết quả của bạn Minh đúng một cách ngẫu nhiên nhưng không thể áp dụng cho phân số có dạng \({{\overline {ab} } \over {\overline {bc} }}\) vì
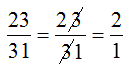
Sai.
Câu 38: Bạn Việt đã tìm ra một vài phân số có tính chất đặc biệt sau đây. Chẳng hạn phân số \({{12} \over {36}}\), nếu đổi chỗ các chữ số ở tử số cũng như ở mẫu thì ta được phân số \({{21} \over {63}}\) và ta có \({{12} \over {36}} = {{21} \over {63}}\). Phân số \({{13} \over {26}}\) cũng có tính chất này. Em thử kiểm tra xem. Em có tìm được 2 phân số khác cũng có tính chất như vậy không?
Advertisements (Quảng cáo)
Ta có \({{13} \over {26}} = {1 \over 2}\) \({{31} \over {62}} = {1 \over 2}\)
Vậy: \({{13} \over {26}} = {{31} \over {62}}\)
Chẳng hạn ta có: \({{12} \over {48}} = {{21} \over {84}}\); \({{14} \over {28}} = {{41} \over {82}}\)
Câu 39: Chứng tỏ rằng \({{12n + 1} \over {30n + 2}}\) là phân số tối giản (n ∈ N).
Advertisements (Quảng cáo)
Ta phải chứng tỏ tử số và mẫu của phân số có ước chung lớn nhất bằng 1 (vì n ∈ N)
Gọi ước chung của 12n+1 và 30n +2 là d, ta chứng minh d = 1
Ta có: (12n+1) ⋮d nên 5.(12n+1) ⋮d
(30n+2) ⋮d nên 2.(30n+2) ⋮d
Suy ra: \(\left[ {5.\left( {12n + 1} \right) – 2.(30n + 2)} \right] \vdots d\)
\( \Rightarrow \) (60n + 5 – 60n – 4) ⋮d
\( \Rightarrow \) 1⋮ d \( \Rightarrow \) d =1
\( \Rightarrow \) Vậy phân số \({{12n + 1} \over {30n + 2}}\) tối giản
Câu 40: Cộng cả tử và mẫu của phân số \({{23} \over {40}}\) với cùng một số tự nhiên n rồi rút gọn, ta được \({3 \over 4}\). Tìm số n.
Ta có phân số mới: \({{23 + n} \over {40 + n}}\) (n ∈ N)
Theo bài ra ta có: \({{23 + n} \over {40 + n}} = {3 \over 4}\)
Nên (23+n).4=3.(40+n)
\( \Rightarrow \) 92+4n = 120+3n
\( \Rightarrow \) 4n-3n= 120-92
\( \Rightarrow \) n = 28
Ta có \({{23 + 28} \over {40 + 28}} = {{51} \over {68}} = {3 \over 4}\)

