Trả lời hoạt động khám phá 1

Độ cao của đáy vịnh Cam Ranh là -32 m. Độ cao của đáy sông Sài Gòn bằng \(\frac{5}{8}\) ở độ cao của đáy vịnh Cam Ranh. Hỏi độ cao của đáy sông Sài Gòn là bao nhiêu mét?

Độ cao của đáy sông Sài Gòn = Độ cao của đáy vịnh Cam Ranh . \(\frac{5}{8}\)

Độ cao của đáy sông Sài Gòn là:
\( – 32.\frac{5}{8} = \frac{{ – 32.5}}{8} = – 20\) (mét)
Thực hành 1

Tính giá trị biểu thức sau theo cách hợp lí.
\(\left( {\frac{{20}}{7}.\frac{{ – 4}}{{ – 5}}} \right) + \left( {\frac{{20}}{7}.\frac{3}{{ – 5}}} \right)\)

Áp dụng tính chất: \(a.b + a.c = a.(b + c)\)

\(\begin{array}{l}\left( {\frac{{20}}{7}.\frac{{ – 4}}{{ – 5}}} \right) + \left( {\frac{{20}}{7}.\frac{3}{{ – 5}}} \right) = \frac{{20}}{7}.\left( {\frac{{ – 4}}{{ – 5}} + \frac{3}{{ – 5}}} \right)\\ = \frac{{20}}{7}.\left( {\frac{{ – 1}}{{ – 5}}} \right) = \frac{{20}}{7}.\frac{1}{5} = \frac{{20}}{{35}} = \frac{4}{7}\end{array}\)
Hoạt động khám phá 2

Một hình chữ nhật có diện tích \(\frac{{48}}{{35}}\) m2 và có chiều dài là \(\frac{6}{5}\) m. Tính chiều rộng của hình chữ nhật đó.

Diện tích hình chữ nhật = Chiều dài x chiều rộng.

Chiều rộng của hình chữ nhật là:
\(\frac{{48}}{{35}}:\frac{6}{5} = \frac{{48}}{{35}}.\frac{5}{6} = \frac{{6.8}}{{7.5}}.\frac{5}{6} = \frac{8}{7}\) (m)
Thực hành 2

Tính.
a) \(\frac{{ – 2}}{7}:\frac{4}{7}\) b) \(\frac{{ – 4}}{5}:\frac{{ – 3}}{{11}}\)
c) \(4:\frac{{ – 2}}{5}\) d) \(\frac{{15}}{{ – 8}}:6\)

Advertisements (Quảng cáo)
\(\frac{a}{b}:\frac{c}{d} = \frac{a}{b}.\frac{d}{c}\)

a) \(\frac{{ – 2}}{7}:\frac{4}{7} = \frac{{ – 2}}{7}.\frac{7}{4} = \frac{{ – 2}}{4} = \frac{{ – 1}}{2}\)
b) \(\frac{{ – 4}}{5}:\frac{{ – 3}}{{11}} = \frac{{ – 4}}{5}.\frac{{11}}{{ – 3}} = \frac{{ – 44}}{{ – 15}} = \frac{{44}}{{15}}\)
c) \(4:\frac{{ – 2}}{5} = 4.\frac{5}{{ – 2}} = \frac{{20}}{{ – 2}} = – 10\)
d) \(\frac{{15}}{{ – 8}}:6 = \frac{{15}}{{ – 8}}.\frac{1}{6} = \frac{{ – 15}}{{48}}\).
Giải bài 1 trang 20 SGK Toán 6 tập 2 Chân trời sáng tạo

Tính giá trị của biểu thức.
a) \(\left( {\frac{{ – 2}}{{ – 5}}:\frac{3}{{ – 4}}} \right).\frac{4}{5}\)
b) \(\frac{{ – 3}}{{ – 4}}:\left( {\frac{7}{{ – 5}}.\frac{{ – 3}}{2}} \right)\)
c) \(\frac{{ – 1}}{9}.\frac{{ – 3}}{5} + \frac{5}{{ – 6}}.\frac{{ – 3}}{5} + \frac{5}{2}.\frac{{ – 3}}{5}.\)

– a,b: Tính theo thứ tự trong ngoặc trước
– c: Áp dụng tính chất phân phối của phép nhân với phép cộng.

a)
Advertisements (Quảng cáo)
\(\begin{array}{l}\left( {\frac{{ – 2}}{{ – 5}}:\frac{3}{{ – 4}}} \right).\frac{4}{5} = \left( {\frac{2}{5}.\frac{{ – 4}}{3}} \right).\frac{4}{5}\\ = \frac{{ – 8}}{{15}}.\frac{4}{5} = \frac{{ – 32}}{{75}}\end{array}\)
b)
\(\begin{array}{l}\frac{{ – 3}}{{ – 4}}:\left( {\frac{7}{{ – 5}}.\frac{{ – 3}}{2}} \right) = \frac{3}{4}:\frac{{ – 21}}{{ – 10}}\\ = \frac{3}{4}.\frac{{10}}{{21}} = \frac{{30}}{{24}} = \frac{5}{4}\end{array}\)
c)
\(\begin{array}{l}\frac{{ – 1}}{9}.\frac{{ – 3}}{5} + \frac{5}{{ – 6}}.\frac{{ – 3}}{5} + \frac{5}{2}.\frac{{ – 3}}{5}.\\ = \frac{{ – 3}}{5}.\left( {\frac{{ – 1}}{9} + \frac{5}{{ – 6}} + \frac{5}{2}} \right)\\ = \frac{{ – 3}}{5}.\left( {\frac{{ – 2}}{{18}} + \frac{{ – 15}}{{18}} + \frac{{45}}{{18}}} \right)\\ = \frac{{ – 3}}{5}.\frac{{28}}{{18}}\\ = \frac{{ – 3}}{5}.\frac{{14}}{9}\\ = \frac{{ – 14}}{{15}}\end{array}\)
Bài 2 trang 20 Toán 6 tập 2 Chân trời sáng tạo

Một ô tô chạy hết 8 phút trên một đoạn đường với vận tốc trung bình 40 km/h. Hãy tính độ dài đoạn đường đó. Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ 5 phút thì ô tô phải chạy với vận tốc trung bình bao nhiêu?

– Tính độ dài quãng đường
=> Vận tốc trung bình nếu muốn chạy hết đoạn đường đó trong 5 phút.

Đổi 8 phút = \(\frac{2}{{15}}\) giờ
5 phút = \(\frac{1}{{12}}\) giờ
Độ dài quãng đường đó là:
\(\frac{2}{{15}}\). 40 = \(\frac{{16}}{3}\) (km)
Người lái xe muốn thời gian chạy hết quãng đường đó chỉ 5 phút thì ô tô phải chạy với vận tốc trung bình là:
\(\frac{{16}}{3}\) : \(\frac{1}{{12}}\) = 64 (km/h)
Đáp số: 64 km/h.
Giải bài 3 trang 21 SGK Toán 6 tập 2 CTST

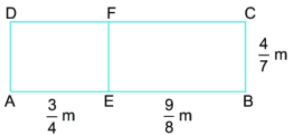
Tính diện tích hình chữ nhật ABCD ở hình bên theo hai cách, trong đó có cách tính tổng diện tích các hình chữ nhật AEFD và EBCF. Hai cách đó minh hoạ tính chất nào của phép nhân A E phân số?

– Cách 1: Tính chiều rộng của hình chữ nhật ABCD sau đó tính diện tích
– Cách 2: Diện tích hình chữ nhật ABCD bằng tổng diện tích hai hình chữ nhật ADFE và BCFE.

Cách 1:
Chiều dài hình chữ nhật ABCD là:
\(\frac{3}{4} + \frac{9}{8} = \frac{{15}}{8}\,(m)\)
Diện tích hình chữ nhật ABCD là:
\(\frac{4}{7}.\frac{{15}}{8} = \frac{{15}}{{14}}\) (m2)
=> Tính chất phân phối của phép nhân.
Cách 2:
Diện tích hình chữ nhật ADFE là:
\(\frac{3}{4}.\frac{4}{7} = \frac{3}{7}\)(m2)
Diện tích hình chữ nhật BCFE là:
\(\frac{4}{7}.\frac{9}{8} = \frac{9}{{14}}\) (m2)
Diện tích hình chữ nhật ABCD là:
\(\frac{3}{7} + \frac{9}{{14}} = \frac{{15}}{{14}}\) (m2)
=> Tính chất kết hợp của phép nhân.