Hoạt động khám phá 1

a) Thuỷ ngân có nhiều công dụng nhưng lại rất độc hại đối với môi trường sống. Thuỷ ngân có nhiệt độ đông đặc là \( – \frac{{3883}}{{100}}\) độ C. Hãy tìm một cách viết khác đơn giản hơn để chỉ nhiệt độ trên.
b) Các phân số \(\frac{{93}}{{10}};\,\frac{{ – 123}}{{100}};\,\frac{{53}}{{1000}};\,\frac{{ – 123}}{{1000}};…\) có thể viết là \(\frac{{93}}{{{{10}^1}}};\,\frac{{ – 123}}{{{{10}^2}}};\,\frac{{53}}{{{{10}^3}}};\,\frac{{ – 123}}{{{{10}^4}}};…\) và gọi là các phân số thập phân.
Em hãy nêu đặc điểm chung của các phân số trên.

a) \( – \frac{{\overline {abcd} }}{{100}} = – \overline {ab,cd} \)
b) Quan sát mẫu số các phân số rồi nhận xét.

a) -38,83 độ C
b) Mẫu số của các phân số trên đều là lũy thừa của 10
Thực hành 1

a) Viết các phân số thập phân sau đây dưới dạng số thập phân:
\(\frac{{37}}{{100}};\,\)\(\frac{{ – 34517}}{{1000}}\); \(\frac{{ – 254}}{{10}}\); \(\frac{{ – 999}}{{10}}\).
b) Viết các số thập phân sau đây dưới dạng phân số thập phân:
2; 2,5; -0,007; -3,053; -7,001; 7,01.

a)
– Các phân số thập phân dương được viết dưới dạng số thập phân dương.
– Các phân số thập phân âm được viết dưới dạng số thập phân âm.
b) Phân số thập phân là phân số có mẫu số là luỹ thừa của 10.

a) \(\frac{{37}}{{100}} = 0,37\); \(\frac{{ – 34517}}{{1000}} = – 34,517\)
\(\frac{{ – 254}}{{10}} = – 25,4\); \(\frac{{ – 999}}{{10}} = – 99,9\)
b) \(2 = \frac{2}{1}\); \(2,5 = \frac{{15}}{{10}}\)
\( – 0,007 = \frac{{ – 7}}{{1000}}\); \( – 3,053 = \frac{{ – 3053}}{{1000}}\)
\( – 7,001 = \frac{{ – 7001}}{{1000}}\); \(7,01 = \frac{{701}}{{100}}\).
Hoạt động khám phá 2

Tìm số đối của \(\frac{{25}}{{10}}\) và viết cả hai số này dưới dạng số thập phân.

Số đối của số a là – a

Số đối của \(\frac{{25}}{{10}}\) là \(\frac{{ – 25}}{{10}}\)
Ta có: \(\frac{{25}}{{10}} = 2,5;\,\,\frac{{ – 25}}{{10}} = – 2,5\)
Thực hành 2

Tìm số đối của các số thập phân sau:
Advertisements (Quảng cáo)
7,02; – 28,12; – 0,69; 0,999.

Số đối của số a là – a

Số đối của \(7,02\) là \( – 7,02\)
Số đối của \( – 0,69\) là \(0,69\)
Số đối của \(0,999\) là \( – 0,999\).
Hoạt động khám phá 3

Viết các số sau đây dưới dạng phân số thập phân và sắp xếp các số đó theo thứ tự từ bé đến lớn.
11,34; 9,35; – 11,34; – 9,35.

Phân số thập phân là phân số có mẫu số là luỹ thừa của 10.

\(11,34 = \frac{{1134}}{{100}}\) \(9,35 = \frac{{935}}{{100}}\)
\( – 11,34 = \frac{{1134}}{{100}}\) \( – 9,35 = \frac{{ – 935}}{{100}}\).
Sắp xếp: \( – 11,34;\,\, – 9,35;\,\,9,35;\,\,11,34\)
Thực hành 3

a) Hãy sắp xếp các số thập phân sau theo thứ tự tăng dần:
-12,13; -2,4; 0,5; -2,3; 2,4.
b) Hãy sắp xếp các số thập phân sau theo thứ tự giảm dần:
-2,9; -2,999; 2,9; 2,999.

Advertisements (Quảng cáo)
So sánh các số rồi viết chúng theo thứ tự tăng dần.

a) -12,13; -2,4; -2,3; 0,5; 2,4
b) 2,999; 2,9; -2,9; -2,999
Trả lời vận dụng

Hãy sắp xếp nhiệt độ đông đặc của các chất sau từ thấp đến cao:
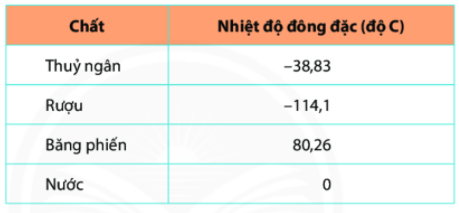

So sánh nhiệt độ đông đặc của các chất rồi sắp xếp nhiệt độ đông đặc của các chất sau từ thấp đến cao.

Ta có: \( – 114,1 < – 38,83 < 0 < 80,26\)
Sắp xếp: Rượu, thủy ngân, nước, băng phiến.
Giải bài 1 trang 31 Toán 6 tập 2 Chân trời sáng tạo

Viết các phân số sau đây dưới dạng số thập phân
\(\frac{{ – 3519}}{{100}};\,\frac{{ – 778}}{{10}};\,\,\frac{{ – 23}}{{1000}};\,\frac{{88}}{{100}}\).

– Các phân số thập phân dương được viết dưới dạng số thập phân dương.
– Các phân số thập phân âm được viết dưới dạng số thập phân âm.

\(\begin{array}{l}\frac{{ – 3519}}{{100}} = – 35,19;\,\,\,\frac{{ – 778}}{{10}} = – 77,8;\\\,\,\frac{{ – 23}}{{1000}} = – 0,023;\,\,\frac{{88}}{{100}} = 0,88\end{array}\).
Bài 2 trang 31 Toán 6 tập 2 CTST

Viết các số thập phân sau đây dưới dạng phân số thập phân
– 312,5; 0,205; – 10,09; – 1,110.

Phân số thập phân là phân số có mẫu số là luỹ thừa của 10.

\(\begin{array}{l} – {\rm{ }}312,5 = \frac{{ – 3125}}{{10}};\;{\rm{ }}0,205 = \frac{{205}}{{1000}};\;{\rm{ }}\\ – {\rm{ }}10,09 = \frac{{ – 1009}}{{100}};\;{\rm{ }} – {\rm{ }}1,110 = \frac{{ – 1110}}{{1000}}.\end{array}\).
Bài 3 trang 31 Toán 6 Chân trời sáng tạo tập 2

Tìm số đối của các số thập phân sau:
9,32; -12,34; -0,7; 3,333

Số đối của số a là – a.

Số đối của 9,32 là -9,32
Số đối của -12,34 là 12,34
Số đối của -0,7 là 0,7
Số đối của 3,333 là -3,333.
Bài 4 trang 32 Toán 6 tập 2 CTST

Hãy sắp xếp các số thập phân sau theo thứ tự tăng dần:
– 2,99; – 2,9; 0,7; 1; 22,1.

So sánh các số rồi sắp xếp các số thập phân sau theo thứ tự tăng dần.

Sắp xếp: -2,99; -2,9; 0,7; 1; 22,1.
Bài 5 trang 32 Toán 6 tập 2 sách Chân trời sáng tạo

Hãy sắp xếp các số sau theo thứ tự giảm dần
0,6; \(\frac{{ – 5}}{6}\); \(\frac{{ – 4}}{3}\); 0; \(\frac{8}{{13}}\); -1,75.

So sánh các số âm và các số dương rồi sắp xếp các số thập phân sau theo thứ tự giảm dần.

Ta có: \(\frac{8}{{13}} = \frac{{80}}{{130}}\); \(0,6 = \frac{6}{{10}} = \frac{{78}}{{130}}\)
Nên \(\frac{8}{{13}} > 0,6\)
Ta có: \(\frac{{ – 5}}{6} = \frac{{ – 20}}{{24}}\); \(\frac{{ – 4}}{3} = \frac{{ – 32}}{{24}}\); \( – 1,75 = \frac{{ – 175}}{{100}} = \frac{{ – 7}}{4} = \frac{{ – 42}}{{24}}\)
Nên: \(\frac{{ – 5}}{6}\)> \(\frac{{ – 4}}{3}\)> -1,75.
=> Sắp xếp: \(\frac{8}{{13}}\); 0,6; 0; \(\frac{{ – 5}}{6}\); \(\frac{{ – 4}}{3}\); -1,75

