Bài 2.9: Vẽ đồ thị của hai hàm số sau trên cùng một hệ trục tọa độ:
\(y = {x^6}\) và \(y = {x^{ – 6}}\)
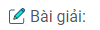
* Xét hàm số y = x6
Tập xác định D = R. Hàm số đã cho là hàm số chẵn.
\(\eqalign{
& y’ = 6{x^5} \cr
& \mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to + \infty } = + \infty \cr} \)
Đồ thị không có tiệm cận
Bảng biến thiên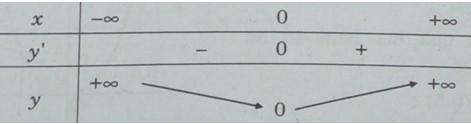
* Xét hàm số \(y = {x^{ – 6}}\)
Tập xác định: D = R\{0}. Hàm số đã cho là hàm số chẵn.
\(\eqalign{
& y’ = – 6{x^{ – 7}} \cr
& \mathop {\lim }\limits_{x \to {0^ – }} y = \mathop {\lim }\limits_{x \to {0^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to + \infty } y = 0 \cr} \)
Advertisements (Quảng cáo)
Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.
Bảng biến thiên: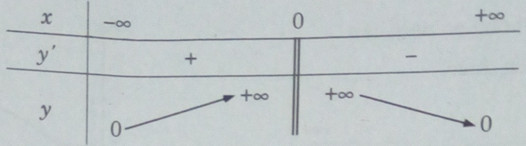 
Đồ thị của các hàm số \(y = {x^6},y = {x^{ – 6}}\) như sau. Các đồ thị này đều có trục đối xứng là trục tung.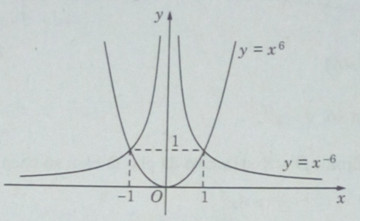
Bài 2.10: Vẽ đồ thị của các hàm số \(y = {x^2}\) và \(y = {x^{{1 \over 2}}}\) trên cùng một hệ trục tọa độ. Hãy so sánh giá trị của các hàm số đó khi \(x = 0,5;1;{3 \over 2};2;3;4.\)
Đặt \(f(x) = {x^2},x \in R\)
Advertisements (Quảng cáo)
\(g(x) = {x^{{1 \over 2}}} = \sqrt x ,x > 0\)
Đồ thị:
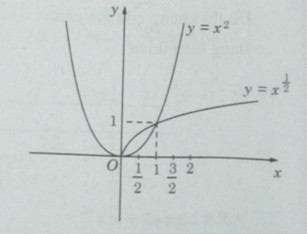Từ đồ thị của hai hình đó ta có:
\(\begin{array}{l}
f(0,5) < g(0,5)\\
f(1) = g(1) = 1;f(\frac{3}{2}) > g(\frac{3}{2})f(2) > g(2);\\
f(3) > g(3),f(4) > g(4)
\end{array}\)
Bài 2.11: Hãy viết các số sau theo thứ tự tăng dần:
a) \({(0,3)^\pi },{(0,3)^{0,5}},{(0,3)^{\frac{2}{3}}},{(0,3)^{3,1415}}\)
b) \(\sqrt {{2^\pi }} ,{(1,9)^\pi },{(\frac{1}{{\sqrt 2 }})^\pi },{\pi ^\pi }\)
c) \({5^{ – 2}},{5^{ – 0,7}},{5^{\frac{1}{3}}},{(\frac{1}{5})^{2,1}}\)
d) \({(0,5)^{ – \frac{2}{3}}},{(1,3)^{ – \frac{2}{3}}},{\pi ^{ – \frac{2}{3}}},{(\sqrt 2 )^{ – \frac{2}{3}}}\)
a) \({(0,3)^\pi };{(0,3)^{3,1415}};{(0,3)^{\frac{2}{3}}};{(0,3)^{0,5}}\)
(vì cơ số a = 0,3 < 1 và \(\pi > 3,1415 > \frac{2}{3} > 0,5\) )
b) \({(\frac{1}{{\sqrt 2 }})^\pi };{(\sqrt 2 )^\pi };{(1,9)^\pi };{\pi ^\pi }\) (vì \(\frac{1}{{\sqrt 2 }} < \sqrt 2 < 1,9 < \pi \) )
c) \({(\frac{1}{5})^{2,1}};{5^{ – 2}};{5^{ – 0,7}};{5^{\frac{1}{3}}}\)
d) \({\pi ^{ – \frac{2}{3}}};{(\sqrt 2 )^{ – \frac{2}{3}}};{(1,3)^{ – \frac{2}{3}}};{(0,5)^{ – \frac{2}{3}}}\).\
