Bài 66
Giải các phương trình sau:
a) \({2^{x + 1}}{.5^x} = 200\);
b) \(0,{125.4^{2x – 3}} = {\left( {4\sqrt 2 } \right)^x}\)
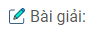
a) \({2^{x + 1}}{.5^x} = 200 \Leftrightarrow {2.2^x}{.5^x} = 200\)
\(\Leftrightarrow {10^x} = 100 \Leftrightarrow x = 2\)
Vậy \(S = \left\{ 2 \right\}\)
b) \(0,{125.4^{2x – 3}} = {\left( {4\sqrt 2 } \right)^x} \Leftrightarrow {1 \over 8}{.2^{2\left( {2x – 3} \right)}} = {\left( {{2^{{5 \over 2}}}} \right)^x} \)
\(\Leftrightarrow {2^{4x – 6 – 3}} = {2^{{{5x} \over 2}}}\)
\( \Leftrightarrow 4x – 9 = {{5x} \over 2} \Leftrightarrow 3x = 18 \Leftrightarrow x = 6\)
Advertisements (Quảng cáo)
Vậy \(S = \left\{ 6 \right\}\)
Bài 67
a) \({\log _2}x + {\log _4}x = {\log _{{1 \over 2}}}\sqrt 3 \);
b) \({\log _{\sqrt 3 }}x.{\log _3}x.{\log _9}x = 8\)
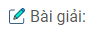
a) Điều kiện: x > 0.
\({\log _2}x + {\log _4}x = {\log _{{1 \over 2}}}\sqrt 3 \)
Advertisements (Quảng cáo)
\(\Leftrightarrow {\log _2}x + {\log _{{2^2}}}x = {\log _{{2^{ – 1}}}}\sqrt 3 \)
\(\eqalign{
& \Leftrightarrow {\log _2}x + {1 \over 2}{\log _2}x = – {\log _2}\sqrt 3\cr& \Leftrightarrow {3 \over 2}{\log _2}x = {\log _2}{1 \over {\sqrt 3 }} \cr
& \Leftrightarrow {\log _2}x = {\log _2}{\left( {{1 \over {\sqrt 3 }}} \right)^{{2 \over 3}}} \Leftrightarrow x = {1 \over {\root 3 \of 3 }} \cr} \)
Vậy \(S = \left\{ {1 \over{\root 3 \of 3 }} \right\}\)
b) Điều kiện: \(x > 0\).
\(\eqalign{
& {\log _{\sqrt 3 }}x.{\log _3}x.{\log _9}x = 8 \cr&\Leftrightarrow {\log _{{3^{{1 \over 2}}}}}x.{\log _3}x.{\log _{{3^2}}}x = 8 \cr
& \Leftrightarrow {1 \over {{1 \over 2}}}.{1 \over 2}.{\left( {{{\log }_3}x} \right)^3} = 8 \cr&\Leftrightarrow {\log _3}x = 2 \Leftrightarrow x = {3^2} = 9 \cr} \)
Vậy \(S = \left\{ 9 \right\}\)
Bài 68
a) \({3^{x + 1}} + {18.3^{ – x}} = 29\);
b) \({27^x} + {12^x} = {2.8^x}\)
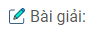( Chia cả hai vế cho \({2^{3x}}\) rồi đặt \(t = {\left( {{3 \over 2}} \right)^x}\))
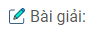
a) Đặt \(t = {3^x}\,\left( {t > 0} \right)\)
Phương trình đã cho trở thành:
\(3t + {{18} \over t} = 29 \Leftrightarrow 3{t^2} – 29t + 18 \Leftrightarrow \left[ \matrix{
t = 9 \hfill \cr
t = {2 \over 3} \hfill \cr} \right.\)
\(\eqalign{
& *\,\,t = 9 \Leftrightarrow {3^x} = 9 \Leftrightarrow x = 2 \cr
& *\,\,t = {2 \over 3} \Leftrightarrow {3^x} = {2 \over 3} \Leftrightarrow x = {\log _3}{2 \over 3} = {\log _3}2 – 1 \cr} \)
Vậy \(S = \left\{ {2;{{\log }_3}2 – 1} \right\}\)
b) Chia hai vế cho \({2^{3x}}\) ta được: \({{{3^{3x}}} \over {{2^{3x}}}} + {{{{12}^x}} \over {{8^x}}} = 2 \Leftrightarrow {\left( {{3 \over 2}} \right)^{3x}} + {\left( {{3 \over 2}} \right)^x} = 2\)
Đặt \(t = {\left( {{3 \over 2}} \right)^x}\,\,\left( {t > 0} \right)\) ta có:
\({t^3} + t – 2 = 0 \Leftrightarrow \left( {t – 1} \right)\left( {{t^2} + t + 2} \right) = 0 \)
\(\Leftrightarrow t = 1 \Leftrightarrow {\left( {{3 \over 2}} \right)^x} = 1 \Leftrightarrow x = 0\)
Vậy \(S = \left\{ 0 \right\}\)
