Bài 57 : Trên hình bên cho hai đường cong (\({C_1}\)) (đường nét liền) và (\({C_2}\)) (đường nét đứt) được vẽ trên cùng một mặt phẳng tọa độ. Biết rằng mỗi đường cong ấy là đồ thị của ột trong hai hàm số lũy thừa \(y = {x^{ – 2}}\) và \(y = {x^{ – {1 \over 2}}}\,\,\left( {x > 0} \right)\). Chỉ dựa vào tính chất của lũy thừa, có thể nhận biết đường cong nào là đồ thị của hàm số nào được không?
Hãy nêu rõ lập luận.
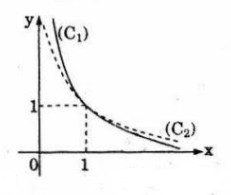
Giả sử (\({C_1}\)) và (\({C_2}\)) theo thứ tự là đồ thị của hàm số \(y = {x^\alpha }\) và \(y = {x^\beta }\) ( \(\alpha \) và \(\beta \) là -2 hoặc \( – {1 \over 2}\)). Trên đồ thị, ta thấy trên khoảng \(\left( {1; + \infty } \right)\), đường cong (\({C_2}\))nằm trên đường cong (\({C_1}\)), nghĩa là khi x > 1 ta có bất đẳng thức \({x^\beta } > {x^\alpha }\). Vậy \(\beta = – {1 \over 2}\) và \(\alpha = – 2\).
Vậy đường (\({C_1}\)) là đồ thị của hàm số \(y = {x^{ – 2}}\), (\({C_2}\)) là đồ thị hàm số \(y = {x^{ – {1 \over 2}}}\).
Bài 58 : Tìm đạo hàm của các hàm số sau:
a) \(y = {\left ( {2x + 1} \right)^\pi }\)
b) \(y = \root 5 \of {{{\ln }^3}5x} \)
Advertisements (Quảng cáo)
c) \(y = \root 3 \of {{{1 + {x^3}} \over {1 – {x^3}}}} \)
d) \(y = {\left( {{x \over b}} \right)^a}{\left( {{a \over x}} \right)^b}\) với a > 0, b> 0
Advertisements (Quảng cáo)
a) \(y’ = 2\pi {\left( {2x + 1} \right)^{\pi – 1}}\)
b) Áp dụng: \(\left( {\root n \of u } \right)’ = {u \over {n\root n \of {{u^{n – 1}}} }}\)
\(y’ = {{\left( {{{\ln }^3}5x} \right)’} \over {5\root 5 \of {{{\left( {{{\ln }^3}5x} \right)}^4}} }} = {{3{{\ln }^2}5x} \over {5x\root 5 \of {{{\ln }^{12}}5x} }}\)
c) Đặt \(u = {{1 + {x^3}} \over {1 – {x^3}}};\,\,y’ = {{u’} \over {3\root 3 \of {{u^2}} }}\)
\(u’ = {{3{x^2}\left( {1 – {x^3}} \right) – 3{x^2}\left( {1 + {x^3}} \right)} \over {{{\left( {1 – {x^3}} \right)}^2}}} = {{6{x^2}} \over {{{\left( {1 – {x^3}} \right)}^2}}}\)
Do đó: \(y’ = {{2{x^2}} \over {{{\left( {1 – {x^3}} \right)}^2}}}.{1 \over {\root 3 \of {{{\left( {{{1 + {x^3}} \over {1 – {x^3}}}} \right)}^2}} }} = {{2{x^2}} \over {\root 3 \of {{{\left( {1 – {x^3}} \right)}^4}{{\left( {1 + {x^3}} \right)}^2}} }}\)
d)
\(\eqalign{
& y’ = \left[ {{{\left( {{x \over b}} \right)}^a}} \right]'{\left( {{a \over x}} \right)^b} + {\left( {{x \over b}} \right)^a}\left[ {{{\left( {{a \over x}} \right)}^b}} \right]’ \cr
& \,\,\,\,\,\, = {a \over b}{\left( {{x \over a}} \right)^{a – 1}}{\left( {{a \over x}} \right)^b} + {\left( {{x \over b}} \right)^a}b{\left( {{a \over x}} \right)^{b – 1}}\left( { – {a \over {{x^2}}}} \right)\cr&\,\,\,\,\,\, = {\left( {{x \over b}} \right)^a}{\left( {{a \over x}} \right)^b}{{a – b} \over x} \cr} \)
Bài 59: Tính giá trị gần đúng đạo hàm của mỗi hàm số sau tại điểm đã cho (chính xác đến hàng phần trăm):
a) \(y = {\log _3}\left( {\sin x} \right)\,\,tai\,x = {\pi \over 4}\,;\)
b) \(y = {{{2^x}} \over {{x^2}}}\,\,tai\,\,x = 1\)
a) \(y’ = {{\cos x} \over {\sin x}}.{1 \over {\ln 3}} = {{\cot x} \over {\ln 3}};\,\,\,y’\left( {{\pi \over 4}} \right) \approx 0,91\)
b) \(y’ = {{{2^x}\left( {x\ln 2 – 2} \right)} \over {{x^3}}};\,\,\,\,y’\left( 1 \right) \approx – 2,61\)

