Bài 5: Đơn giản biểu thức ( với a, b là những số dương)
a) \({{{{\left( {\root 4 \of {{a^3}{b^2}} } \right)}^4}} \over {\root 3 \of {\sqrt {{a^{12}}{b^6}} } }}\)
b) \({{{a^{{1 \over 3}}} – {a^{{7 \over 3}}}} \over {{a^{{1 \over 3}}} – {a^{{4 \over 3}}}}} – {{{a^{ – {1 \over 3}}} – {a^{{5 \over 3}}}} \over {{a^{{2 \over 3}}} + {a^{ – {1 \over 3}}}}}\)
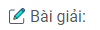
a) \({{{{\left( {\root 4 \of {{a^3}{b^2}} } \right)}^4}} \over {\root 3 \of {\sqrt {{a^{12}}{b^6}} } }} = {{{a^3}{b^2}} \over {\root 6 \of {{a^{12}}{b^6}} }} = {{{a^3}{b^2}} \over {{a^2}b}} = ab\)
b) \({{{a^{{1 \over 3}}} – {a^{{7 \over 3}}}} \over {{a^{{1 \over 3}}} – {a^{{4 \over 3}}}}} – {{{a^{ – {1 \over 3}}} – {a^{{5 \over 3}}}} \over {{a^{{2 \over 3}}} + {a^{ – {1 \over 3}}}}} = {{{a^{{1 \over 3}}}\left( {1 – {a^2}} \right)} \over {{a^{{1 \over 3}}}\left( {1-a} \right)}} – {{{a^{ – {1 \over 3}}}\left( {1 – {a^2}} \right)} \over {{a^{ – {1 \over 3}}}\left( {a + 1} \right)}}\)
\(= \left( {1 + a} \right) – \left( {1 – a} \right) = 2a.\)
Bài 6: So sánh các số
a) \(\sqrt 2 \) và \(\root 3 \of 3 \); b) \(\sqrt 3 + \root 3 \of {30} \) và \(\root 3 \of {63} \);
c) \(\root 3 \of 7 + \sqrt {15} \) và \(\sqrt {10} + \root 3 \of {28} \);
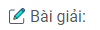
a) Ta có \({\left( {\sqrt 2 } \right)^6} = {2^3} = 8\); \({\left( {\root 3 \of 3 } \right)^6} = {3^2} = 9\)
Do 9>8 nên ta có \({\left( {\sqrt 2 } \right)^6}\) < \({\left( {\root 3 \of 3 } \right)^6}\), suy ra \(\sqrt 2 \) < \(\root 3 \of 3 \).
b) \(\sqrt 3 + \root 3 \of {30} > 1 + \root 3 \of {27} = 4 = \root 3 \of {64} > \root 3 \of {63} \).
c) \(\root 3 \of 7 + \sqrt {15} < 2 + 4 = 3 + 3 < \sqrt {10} + \root 3 \of {28} \).
Advertisements (Quảng cáo)
Bài 7: Chứng minh \(\root 3 \of {7 + 5\sqrt 2 } + \root 3 \of {7 – 5\sqrt 2 } = 2\)
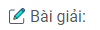
Đặt \(x = \root 3 \of {7 + 5\sqrt 2 } + \root 3 \of {7 – 5\sqrt 2 } \) Ta có:
\({x^3} = \left( {\root 3 \of {7 + 5\sqrt 2 } + \root 3 \of {7 – 5\sqrt 2 } } \right)^3\)
\( = 7 + 5\sqrt 2 + 7 – 5\sqrt 2 \)
\(+ 3\root 3 \of {{{\left( {7 + 5\sqrt 2 } \right)}^2}} .\root 3 \of {7 – 5\sqrt 2 } \)
\(+ 3\root 3 \of {7 + 5\sqrt 2 } .\root 3 \of {{{\left( {7 – 5\sqrt 2 } \right)}^2}} \)
\( = 14 – 3\left( {\root 3 \of {7 + 5\sqrt 2 } + \root 3 \of {7 – 5\sqrt 2 } } \right) = 14 – 3x\).
Từ đó suy ra: \({x^3} + 3x – 14 = 0\,\,\,\,\left( 1 \right)\)
Advertisements (Quảng cáo)
\(\left( 1 \right) \Leftrightarrow \left( {x – 2} \right)\left( {{x^2} + 2x + 7} \right) = 0 \)
\(\Leftrightarrow x – 2 = 0 \Leftrightarrow x = 2\) ( vì \({x^2} + 2x + 7 > 0\))
Vậy \(\root 3 \of {7 + 5\sqrt 2 } + \root 3 \of {7 – 5\sqrt 2 } = 2\)
Bài 8: Đơn giản biểu thức:
a) \({{\sqrt a – \sqrt b } \over {\root 4 \of a – \root 4 \of b }} – {{\sqrt a + \root 4 \of {ab} } \over {\root 4 \of a + \root 4 \of b }}\);
b) \({{a – b} \over {\root 3 \of a – \root 3 \of b }} – {{a + b} \over {\root 3 \of a + \root 3 \of b }}\);
c) \(\left( {{{a + b} \over {\root 3 \of a + \root 3 \of b }} – \root 3 \of {ab} } \right):{\left( {\root 3 \of a – \root 3 \of b } \right)^2};\)
d) \({{a – 1} \over {{a^{{3 \over 4}}} + {a^{{1 \over 2}}}}}.{{\sqrt a + \root 4 \of a } \over {\sqrt a + 1}}.{a^{{1 \over 4}}} + 1.\)
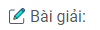
a) \({{\sqrt a – \sqrt b } \over {\root 4 \of a – \root 4 \of b }} – {{\sqrt a + \root 4 \of {ab} } \over {\root 4 \of a + \root 4 \of b }} = {{\left( {\root 4 \of a + \root 4 \of b } \right)\left( {\root 4 \of a – \root 4 \of b } \right)} \over {\root 4 \of a – \root 4 \of b }} – {{\root 4 \of a \left( {\root 4 \of a + \root 4 \of b } \right)} \over {\root 4 \of a + \root 4 \of b }}\)
\( = \root 4 \of a + \root 4 \of b – \root 4 \of a = \root 4 \of b \)
b) \({{a – b} \over {\root 3 \of a – \root 3 \of b }} – {{a + b} \over {\root 3 \of a + \root 3 \of b }} = {{{{\left( {\root 3 \of a } \right)}^3} – {{\left( {\root 3 \of b } \right)}^3}} \over {\root 3 \of a – \root 3 \of b }} – {{{{\left( {\root 3 \of a } \right)}^3} + {{\left( {\root 3 \of b } \right)}^3}} \over {\root 3 \of a + \root 3 \of b }}\)
\( = \root 3 \of {{a^2}} + \root 3 \of {ab} + \root 3 \of {{b^2}} – \left( {\root 3 \of {{a^2}} – \root 3 \of {ab} + \root 3 \of {{b^2}} } \right)\)
\(= 2\root 3 \of {ab} \)
c) \(\left( {{{a + b} \over {\root 3 \of a + \root 3 \of b }} – \root 3 \of {ab} } \right):{\left( {\root 3 \of a – \root 3 \of b } \right)^2} \)
\(= \left( {\root 3 \of {{a^2}} – \root 3 \of {ab} + \root 3 \of {{b^2}} – \root 3 \of {ab} } \right):{\left( {\root 3 \of a – \root 3 \of b } \right)^2}\)
\( = \left( {\root 3 \of {{a^2}} – 2\root 3 \of {ab} + \root 3 \of {{b^2}} } \right):{\left( {\root 3 \of a – \root 3 \of b } \right)^2}\)
\(= {\left( {\root 3 \of a – \root 3 \of b } \right)^2}:{\left( {\root 3 \of a – \root 3 \of b } \right)^2} = 1\)
d) \({{a – 1} \over {{a^{{3 \over 4}}} + {a^{{1 \over 2}}}}}.{{\sqrt a + \root 4 \of a } \over {\sqrt a + 1}}.{a^{{1 \over 4}}} + 1. \)
\(= {{\left( {\sqrt a + 1} \right)\left( {\sqrt a – 1} \right)} \over {\sqrt a \left( {\root 4 \of a + 1} \right)}}.{{\root 4 \of a \left( {\root 4 \of a + 1} \right)} \over {\left( {\sqrt a + 1} \right)}}.\root 4 \of a + 1\)
\( = \sqrt a – 1 + 1 = \sqrt a \)

