Bài 29: Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x = -1\) và \(x = 1\), biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x( – 1 \le x \le 1)\) là một hình vuông cạnh là \(2\sqrt {1 – {x^2}} \).
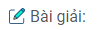
\(S(x) = {(2\sqrt {1 – {x^2}} )^2} = 4(1 – {x^2})\)
Ta có: \(V = \int\limits_{ – 1}^1 {4(1 – {x^2})dx = } \left. {\left( {4x – {{4{x^3}} \over 3}} \right)} \right|_{ – 1}^1 = {{16} \over 3}.\)
Bài 30: Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x = 0\) và \(x = \pi \), biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\;(0 \le x \le \pi )\) là một tam giác đều cạnh \(2\sqrt {{\mathop{\rm s}\nolimits} {\rm{inx}}} \).
Advertisements (Quảng cáo)
Ta có: \(S(x) = {(2\sqrt {{\mathop{\rm s}\nolimits} {\rm{inx}}} )^2}.{{\sqrt 3 } \over 4} = \sqrt 3 {\mathop{\rm s}\nolimits} {\rm{inx}}\)
Do đó: \(V = \int\limits_0^\pi {S(x)dx = \int\limits_0^\pi {\sqrt 3 } } \sin {\rm{x}}dx = – \sqrt 3 \cos x\mathop |\nolimits_0^\pi \)
\(= 2\sqrt 3 \)
Bài 31: Cho hình phẳng \(A\) giới hạn bởi các đường \(y = 0, x = 4\), và \(y = \sqrt x – 1\). Tính thể tích của khối tròn xoay tạo thành khi quay hình \(A\) quanh trục hoành.
Advertisements (Quảng cáo)
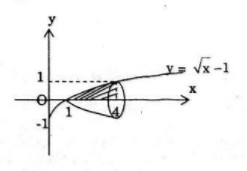
Hoành độ giao điểm của đường thẳng với trục hoành
\(\eqalign{
& \sqrt x – 1 = 0 \Leftrightarrow x = 1 \cr
& V = \pi \int\limits_1^4 {{{(\sqrt x – 1)}^2}} dx = \pi \int\limits_1^4 {(x – 2\sqrt x } + 1)dx\cr& = \left. {\pi \left( {{{{x^2}} \over 2} – {4 \over 3}x\sqrt x + x} \right)} \right|_1^4 = {{7\pi } \over 6} \cr} \)
Bài 32: Cho hình phẳng B giới hạn bởi các đường \(x = {2 \over y},y = 1\) và \(y=4\). Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.
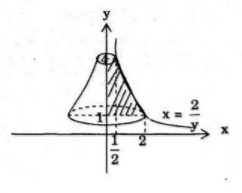
Ta có \(V = \pi {\int\limits_1^4 {\left( {{2 \over y}} \right)} ^2}dy = 4\pi \int\limits_1^4 {{{dy} \over {{y^2}}}} = \left. {4\pi \left( { – {1 \over y}} \right)} \right|_1^4 = 3\pi \)

