Bài 4: Chứng minh rằng với mọi giá trị của tham số \(m\), hàm số
\(y{\rm{ }} = {\rm{ }}{x^3}-{\rm{ }}m{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1\)
luôn luôn có một điểm cực đại và một điểm cực tiểu.
\(y{\rm{ }} = {\rm{ }}3{x^2}-{\rm{ }}2mx{\rm{ }}-{\rm{ }}2{\rm{ }},\Delta ‘ = {\rm{ }}{m^{2}} + {\rm{ }}6{\rm{ }} > {\rm{ }}0\) nên \(y’ = 0\) có hai nghiệm phân biệt và \(y’\) đổi dấu khi qua các nghiệm đó.
Vậy hàm số luôn có một cực đại và một cực tiểu.
Bài 5: Tìm \(a\) và \(b\) để các cực trị của hàm số
\(y=\frac{5}{3}a^{2}x^{3}+2ax^{2}-9x+b\)
đều là những số dương và \(x_{0}=-\frac{5}{9}\) là điểm cực đại.
– Xét \(a = 0\) hàm số trở thành \(y = -9x + b\). Trường hợp này hàm số không có cực trị.
– Xét \(a \ne 0\). Ta có : \(y{\rm{ }} = {\rm{ }}5{a^2}{x^2} + {\rm{ }}4ax{\rm{ }}-{\rm{ }}9\); \(y’= 0 \)\(⇔ x=-\frac{1}{a}\) hoặc \(x=-\frac{9}{5a}\)
– Với \(a < 0\) ta có bảng biến thiên :
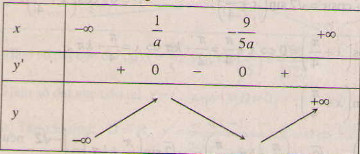
Advertisements (Quảng cáo)
Theo giả thiết \(x_{0}=-\frac{5}{9}\) là điểm cực đại nên \(\frac{1}{a}=-\frac{5}{9}\Leftrightarrow a=\frac{9}{5}\). Theo yêu cầu bài toán thì
\(y_{(CT)}=y\left ( -\frac{9}{5a} \right )=y(1)>0\)
\(\Leftrightarrow \frac{5}{3}\cdot \left ( -\frac{9}{5} \right )^{2}+2\cdot \left ( -\frac{9}{5} \right )-9+b>0\Leftrightarrow b>\frac{36}{5}.\)
– Với \(a > 0\) ta có bảng biến thiên :
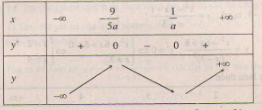
Vì \(x_{0}=-\frac{5}{9}\) là điểm cực đại nên \(-\frac{9}{5a}=-\frac{5}{9}\Leftrightarrow a=\frac{81}{25}\). Theo yêu cầu bài toán thì: \(y_{(ct)}=y\left ( \frac{1}{a} \right )=y\left ( \frac{25}{81} \right )>0\)
\(\Leftrightarrow \frac{5}{3}\cdot \left ( \frac{81}{25} \right )^{2}\left ( \frac{25}{81} \right )^{3}+2.\frac{81}{25}\cdot \left ( \frac{25}{81} \right )^{2}-9\cdot \frac{25}{81}+b>0\)
\(\Leftrightarrow b>\frac{400}{243}.\)
Advertisements (Quảng cáo)
Vậy các giá trị \(a, b\) cần tìm là:
\(\left\{\begin{matrix} a=-\frac{9}{5} & \\ b>\frac{36}{5} & \end{matrix}\right.\) hoặc \(\left\{\begin{matrix} a=\frac{81}{25} & \\ b>\frac{400}{243} & \end{matrix}\right.\).
Bài 6 trang 18 sách sgk giải tích 12
Xác định giá trị của tham số \(m\) để hàm số \(y=\frac{x^{2}+mx+1}{x+m}\) đạt cực đại tại \(x = 2\).
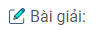
Tập xác định : \(D=\mathbb{R}\setminus \left \{ -m \right \};\)
\(y’=\frac{2x^{2}+2mx+m^{2}-1}{(x+m)^{2}}.\)
Nếu hàm số đạt cực đại tại \(x = 2\) thì \(y'(2) = 0\) \(⇔ {m^{2}} + {\rm{ }}4m{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}0\)\( ⇔ m=-1\) hoặc \(m=-3\)
– Với \(m = -1\), ta có : \(y=\frac{x^{2}-x+1}{x-1};\)
\(y’=\frac{x^{2}-2x}{(x-1)^{2}}; y’=0\Leftrightarrow \left\{\begin{matrix} x^{2} -2x=0& \\ x\neq 1 & \end{matrix}\right.\)
\(\Leftrightarrow x=0\) hoặc \(x=2\).
Ta có bảng biến thiên :

Trường hợp này ta thấy hàm số không đạt cực đại tại \(x = 2\).
– Với \(m = -3\), ta có: \(y=\frac{x^{2}3x+1}{x-3};\)
\(y’=\frac{x^{2}-6x+8}{(x-3)^{2}};y’=0\Leftrightarrow \left\{\begin{matrix} x^{2-6x+8=0} & \\ x\neq 3 & \end{matrix}\right.\)
\(\Leftrightarrow x=2\) hoặc \(x=4\)
Ta có bảng biến thiên :
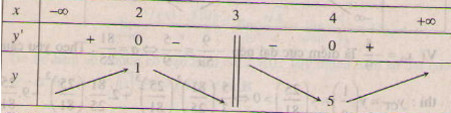
Trường hợp này ta thấy hàm số đạt cực đại tại \(x = 2\).
Vậy \(m = -3\) là giá trị cần tìm.

