Bài 4 trang 126 SGK Giải tích 12: Tính:
a) \(\int {(2 – x)\sin {\rm{x}}dx} \)
b) \(\int {{{{{(x + 1)}^2}} \over {\sqrt x }}} dx\)
c) \(\int {{{{e^{3x}} + 1} \over {{e^x} + 1}}} dx\)
d) \(\int {{1 \over {{{(\sin x + {\mathop{\rm cosx}\nolimits} )}^2}}}} dx\)
e) \(\int {{1 \over {\sqrt {1 + x} + \sqrt x }}} dx\)
g) \(\int {{1 \over {(x + 1)(2 – x)}}} dx\)
a) Đặt \(u = 2 – x, dv = sinx dx\)
Ta có: \(du = -dx, v = -cosx\)
Do đó:
\(\eqalign{
& \int {(2 – x)\sin {\rm{x}}dx} = (x – 2)cosx – \int {{\mathop{\rm cosxdx}\nolimits} } \cr
& = (x – 2)cosx – s{\rm{inx}} + C \cr} \)
b) Điều kiện: \(x > 0\)
Ta có:
\(\eqalign{
& \int {{{{{(x + 1)}^2}} \over {\sqrt x }}} dx = \int {{{{x^2} + 2x + 1} \over {{x^{{1 \over 2}}}}}} dx \cr
& = \int {({x^{{3 \over 2}}}} + 2{x^{{1 \over 2}}} + {x^{{-1 \over 2}}})dx \cr
& = {2 \over 5}{x^{{5 \over 2}}} + {4 \over 3}{x^{{3 \over 2}}} + 2{x^{{1 \over 2}}} + C \cr} \)
c) Ta có: \({e^{3x}} + 1={({e^x})^3} + 1 = ({e^x} + 1)({e^{2x}}-{e^x} +1)\)
Do đó:
\(\eqalign{
& \int {{{{e^{3x}} + 1} \over {{e^x} + 1}}} dx = \int {\left( {{e^{2x}}-{\rm{ }}{e^x} + {\rm{ }}1} \right)} dx \cr
& = {1 \over 2}{e^{2x}} – {e^x} + x + C \cr} \)
d) Ta có:
\(\eqalign{
& \int {{1 \over {{{(\sin x + {\mathop{\rm cosx}\nolimits} )}^2}}}} dx = \int {{{d(x – {\pi \over 4})} \over {2{{\cos }^2}(x – {\pi \over 4})}}} \cr
& = {1 \over 2}\tan (x – {\pi \over 4}) + C \cr} \)
e) Nhân tử và mẫu với biểu thức liên hợp, ta có:
\(\eqalign{
& \int {{1 \over {\sqrt {1 + x} + \sqrt x }}} dx = \int {(\sqrt {1 + x} } – \sqrt x )dx \cr
& = \int {\left[ {{{(1 + x)}^{{1 \over 2}}} – {x^{{1 \over 2}}}} \right]} dx = {2 \over 3}{(x + 1)^{{3 \over 2}}} – {2 \over 3}{x^{{3 \over 2}}} + C \cr} \)
d) Ta có:
\(\eqalign{
& \int {{1 \over {(x + 1)(2 – x)}}} dx = {1 \over 3}\int {({1 \over {1 + x}}} + {1 \over {2 – x}})dx \cr
& = {1 \over 3}\ln |{{1 + x} \over {2 – x}}| + C \cr} \).
Bài 5: Tính:
a) \(\int_0^3 {{x \over {\sqrt {1 + x} }}} dx\)
b) \(\int_1^{64} {{{1 + \sqrt x } \over {\root 3 \of x }}} dx\)
c) \(\int_0^2 {{x^2}} {e^{3x}}dx\)
d) \(\int_0^\pi {\sqrt {1 + \sin 2x} } dx\)
Advertisements (Quảng cáo)
a) Đặt \(t = \sqrt {1 + x} \) , ta được: \(x = t^2- 1, dx = 2t dt\)
Khi \(x = 0\) thì \(t = 1\), khi \(x = 3\) thì \(t = 2\)
Do đó:
\( \int_0^3 {{x \over {\sqrt {1 + x} }}} dx = \int_1^2 {{{{t^2} – 1} \over t}} .2tdt = 2\int_1^2 {({t^2} – 1)dt}\)
\(= 2({{{t^3}} \over 3} – t)\left| {_1^2} \right. = 2({8 \over 3} – 2 – {1 \over 3} + 1) = {8 \over 3} \)
b)
Ta có:
\(\int_1^{64} {{{1 + \sqrt x } \over {\root 3 \of x }}} dx = \int_1^{64} {{{1 + {x^{{1 \over 2}}}} \over {{x^{{1 \over 3}}}}}} dx = \int_1^{64} {({x^{{-1 \over 3}}} + {x^{{1 \over 6}}})dx}\)
\(=({3 \over 2}{x^{{2 \over 3}}} + {6 \over 7}{x^{{7 \over 6}}})\left| {_1^{64}} \right. = {{1839} \over {14}} \)
c) Ta có:
\( \int_0^2 {{x^2}} {e^{3x}}dx = {1 \over 3}\int_0^2 {{x^2}} d{e^{3x}} = {1 \over 3}{x^2}{e^{3x}}\left| {_0^2} \right.\)
\(- {2 \over 3}\int_0^2 {x{e^{3x}}} dx \)\(= {4 \over 3}{e^6} – {2 \over 9}(x{e^{3x}})\left| {_0^2} \right. + {2 \over {27}}\int_0^2 {{e^{3x}}} d(3x) \)
\(= {4 \over 3}{e^6} – {4 \over 9}{e^6} + {2 \over {27}}{e^{3x}}\left| {_0^2} \right. = {2 \over {27}}(13{e^6} – 1) \)
d)
Ta có:
\( \sqrt {1 + \sin 2x} = \sqrt {{{\sin }^2}x + {{\cos }^2}x + 2\sin x{\mathop{\rm cosx}\nolimits} }\)
\(= |{\mathop{\rm s}\nolimits} {\rm{inx}} + {\mathop{\rm cosx}\nolimits} | \)\(= \sqrt 2 |\sin (x + {\pi \over 4})| \)
\(=\left\{ \matrix{
\sqrt 2 \sin (x + {\pi \over 4}),x \in \left[ {0,{{3\pi } \over 4}} \right] \hfill \cr
\sqrt 2 \sin (x + {\pi \over 4}),X \in \left[ {{{3\pi } \over 4},\pi } \right] \hfill \cr} \right.\)
Do đó:
\( \int_0^\pi {\sqrt {1 + \sin 2x} } dx = \sqrt 2 \int_0^{{{3\pi } \over 4}} {\sin (x + {\pi \over 4}} )d(x + {\pi \over 4})\)\( – \sqrt 2 \int_{{{3\pi } \over 4}}^\pi {\sin (x + {\pi \over 4}} )d(x + {\pi \over 4}) \) \(= – \sqrt 2 \cos (x + {\pi \over 4})\left| {_0^{{{3\pi } \over 4}}} \right. + \sqrt 2 (x + {\pi \over 4})\left| {_{{{3\pi } \over 4}}^\pi } \right. = 2\sqrt 2 \)
Bài 6 trang 127 SGK Giải tích 12: Tính:
Advertisements (Quảng cáo)
a) \(\int_0^{{\pi \over 2}} {\cos 2xsi{n^2}} xdx\)
b) \(\int_{ – 1}^1 {|{2^x}} – {2^{ – x}}|dx\)
c) \(\int_1^2 {{{(x + 1)(x + 2)(x + 3)} \over {{x^2}}}} dx\)
d) \(\int_0^2 {{1 \over {{x^2} – 2x – 3}}} dx\)
e) \(\int_0^{{\pi \over 2}} {{{({\mathop{\rm s}\nolimits} {\rm{inx}} + {\mathop{\rm cosx}\nolimits} )}^2}dx} \)
g) \(\int_0^\pi {{{(x + {\mathop{\rm s}\nolimits} {\rm{inx}})}^2}} dx\)
a)
Ta có:
\( \int_0^{{\pi \over 2}} {\cos 2xsi{n^2}} xdx = {1 \over 2}\int_0^{{\pi \over 2}} {\cos 2x(1 – \cos 2x)dx}\)
\(= {1 \over 2}\int_0^{{\pi \over 2}} {\left[ {\cos 2x – {{1 + \cos 4x} \over 2}} \right]} dx\)
\( = {1 \over 4}\int_0^{{\pi \over 2}} {(2\cos 2x – \cos 4x – 1)dx} \)
\( = {1 \over 4}\left[ {\sin 2x – {{\sin 4x} \over 4} – x} \right]_0^{{\pi \over 2}} = – {1 \over 4}.{\pi \over 2} = {{ – \pi } \over 8} \)
b)
Ta có: Xét \({2^x}-{2^{ – x}} ≥ 0 ⇔ x ≥ 0\).
Ta tách thành tổng của hai tích phân:
\(\int_{ – 1}^1 {|{2^x}} – {2^{ – x}}|dx = – \int_{ – 1}^0 ( {2^x} – {2^{ – x}})dx \)\(+ \int_0^1 ( {2^x} – {2^{ – x}})dx\)
\(= – ({{{2^x}} \over {\ln 2}} + {{{2^{ – x}}} \over {\ln 2}})\left| {_{ – 1}^0} \right. + ({{{2^x}} \over {\ln 2}} + {{{2^{ – x}}} \over {\ln 2}})\left| {_0^1} \right. \)\(= {1 \over {\ln 2}} \)
c)
\(\int_1^2 {{{(x + 1)(x + 2)(x + 3)} \over {{x^2}}}} dx = \int_1^2 {{{{x^3} + 6{x^2} + 11x + 6} \over {{x^2}}}dx} \)
\(= \int_1^2 {(x + 6 + {{11} \over x}} + {6 \over {{x^2}}})dx\)
\(= \left[ {{{{x^2}} \over 2} + 6x + 11\ln |x| – {6 \over x}} \right]\left| {_1^2} \right. \)
\( = (2 + 12 + 11\ln 2 – 3) – ({1 \over 2} + 6 – 6) \)
\(= {{21} \over 2} + 11\ln 2 \)
d)
\(\eqalign{
& \int_0^2 {{1 \over {{x^2} – 2x – 3}}} dx = \int_0^2 {{1 \over {(x + 1)(x – 3)}}dx = {1 \over 4}} \int_0^2 {({1 \over {x – 3}} – {1 \over {x + 1}})dx} \cr
& = {1 \over 4}\left[ {\ln |x – 3| – \ln |x + 1|} \right]\left| {_0^2} \right. = {1 \over 4}\left[ {- \ln 3 – \ln 3} \right] \cr
& = {-1 \over 2} \ln 3\cr} \)
e)
\(\eqalign{
& \int_0^{{\pi \over 2}} {{{({\mathop{\rm s}\nolimits} {\rm{inx}} + {\mathop{\rm cosx}\nolimits} )}^2}dx} = \int_0^{{\pi \over 2}} {(1 + \sin 2x)dx} \cr
& = \left[ {x – {{\cos 2x} \over 2}} \right]\left| {_0^{{\pi \over 2}}} \right. = {\pi \over 2} + 1 \cr} \)
g)
\(\eqalign{
& I = \int_0^\pi {{{(x + {\mathop{\rm s}\nolimits} {\rm{inx)}}}^2}} dx\int_0^\pi {({x^2}} + 2x\sin x + {\sin ^2}x)dx \cr
& = \left[ {{{{x^3}} \over 3}} \right]\left| {_0^\pi } \right. + 2\int_0^\pi {x\sin xdx + {1 \over 2}} \int_0^\pi {(1 – \cos 2x)dx} \cr} \)
Tính :\(J = \int_0^\pi {x\sin xdx} \)
Đặt \(u = x ⇒ u’ = 1\) và \(v’ = sinx ⇒ v = -cos x\)
Suy ra:
\(J = \left[ { – x{\mathop{\rm cosx}\nolimits} } \right]\left| {_0^\pi } \right. + \int_0^\pi {{\mathop{\rm cosxdx}\nolimits} = \pi + \left[ {{\mathop{\rm s}\nolimits} {\rm{inx}}} \right]} \left| {_0^\pi } \right. = \pi \)
Do đó:
\(\eqalign{
& I = {{{\pi ^3}} \over 3} + 2\pi + {1 \over 2}\left[ {x – {{\sin 2x} \over 2}} \right]\left| {_0^{{\pi }}} \right. \cr
& = {{{\pi ^3}} \over 3} + 2\pi + {\pi \over 2} = {{2{\pi ^3} + 15\pi } \over 6} \cr} \)
Bài 7: Xét hình phẳng D giới hạn bởi \(y = \sqrt {1 – {x^2}} \) và \(y = 2(1-x)\)
a) Tính diện tích hình D
b) Quay hình D xung quanh trục \(Ox\). Tính thể tích khối tròn xoay được tạo thành.
a) Phương trình hoành độ giao điểm của hai đồ thị là:
\(\eqalign{
& 2\sqrt {1 – {x^2}} = 2(1 – x) \Leftrightarrow \left\{ \matrix{
1 – x \ge 0 \hfill \cr
1 – {x^2} = {(1 – x)^2} \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
x \le 1 \hfill \cr
2{x^2} – 2x = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \le 1 \hfill \cr
\left[ \matrix{
x = 0 \hfill \cr
x = 1 \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 1 \hfill \cr} \right. \cr} \)
Đồ thị của hàm số \(y = \sqrt {1 – {x^2}} \) là một nửa elip \({x^2} + {{{y^2}} \over 4} = 1\) với y ≥ 0
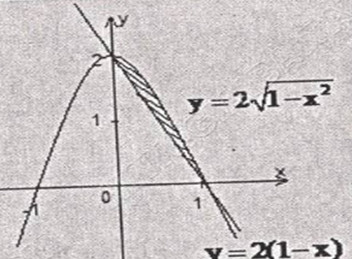
Từ đồ thị trên ta có, diện tích của D:
\(\eqalign{
& S = \int_0^1 {\left[ {2\sqrt {1 – {x^2}} – 2(1 – x)} \right]} dx \cr
& = 2\left[ {\int_0^1 {\sqrt {1 – {x^2}} dx – \int_0^1 {(1 – x)dx} } } \right] \cr} \)
Tính \(\int_0^1 {\sqrt {1 – {x^2}} } dx\) :
Đặt \(x = sin t\) , ta có: \(dx = cost dt\); \(x=0 \Rightarrow t= 0\); \(x=1 \Rightarrow t={\pi \over 2}\)
Suy ra:
\(\eqalign{
& \int_0^1 {\sqrt {1 – {x^2}} } dx = \int_0^{{\pi \over 2}} {\sqrt {1 – {{\sin }^2}t} } .costdt \cr
& = \int_0^{{\pi \over 2}} {{\mathop{\rm cost}\nolimits} .costdt = \int_0^{{\pi \over 2}} {{{\cos }^2}tdt} } \cr
& = {1 \over 2}\int_0^{{\pi \over 2}} {(1 + \cos 2t)dt = {1 \over 2}} \left[ {t + {1 \over 2}\sin 2t} \right]\left| {_0^{{\pi \over 2}}} \right. = {\pi \over 4} \cr
& \int_0^1 {(1 – x)dx = (x – {{{x^2}} \over 2})\left| {_0^1} \right.} = {1 \over 2} \cr
& \Rightarrow D = 2({\pi \over 4} – {1 \over 2}) = {\pi \over 2}-1 \cr} \)
b) Dựa vào hình trêm ta có thể tích cần tìm là:
\(\eqalign{
& V = 4\pi \int_0^1 {\left[ {(1 – {x^2}) – (1 – {x})^2} \right]} dx \cr
& = 8\pi \int_0^1 {(x – {x^2}} )dx = 8\pi\left( {{{{x^2}} \over 2} – {{{x^3}} \over 3}} \right)\left| {_0^1} \right. \cr
& = 8\pi ({1 \over 2} – {1 \over 3}) = {{4\pi } \over 3} \cr} \)

