Bài 1: Thế nào là phần thực, phần ảo, modun của số phức?
Viết công thức tính môdun của một số phức theo phần thực và phần ảo của nó.
– Mỗi biểu thức dạng \(a+bi\), trong đó \(a, b ∈ R, i^2= -1\) được gọi làm một số phức.
– Với số phức \(z = a + bi\), ta gọi \(a\) là phần thực, số \(b\) gọi là phần ảo của \(z\).
– Ta có \(z = a + bi\) thì môdun của \(z\) là \(|z| = |a + bi| = \sqrt {{a^2} + {b^2}} \).
Bài 2: Tìm mối liên hệ giữa khái niệm môdun và khái niệm giá trị tuyệt đối của một số thực.
– Nếu số thực \(x\) là một số thực thì môdun \(x\) chính là giá trị tuyệt đối của số phức \(z\).
Advertisements (Quảng cáo)
– Nếu số phức \(z\) không phải là một số thực thì chỉ có môdun của \(z\), không có khái niệm giá trị tuyệt đối của \(z\).
Bài 3: Nêu định nghĩa số phức liên hợp của số phức \(z\). Số phức nào bằng số phức liên hợp của nó?
*Cho số phức \(z = a + bi\).
Ta gọi số phức \(a – bi\) là số phức liên hợp của \(z\) và kí hiệu là \(\bar z\).
Advertisements (Quảng cáo)
Vậy ta có \(z = a + bi\) thì \(\bar z= a – bi\)
*Số phức \(z\) bằng số phức liên hợp của nó \(⇔ a = a\) và \(b = -b\)
\(⇔ a ∈ R\) và \(b = 0 ⇔ z\) là một số thực.
Bài 4: Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình a), b), c) sau:
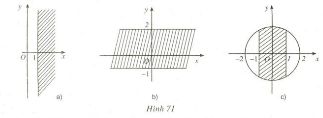
Giả sử \(z = x + yi\) (\(x,y \in \mathbb R\)), khi đó số phức \(z\) được biểu diễn bởi điểm \(M(x, y)\) trên mặt phẳng tọa độ \(Oxy\).
a) Trên hình 71.a (SGK), điểm biểu diễn ở phần gạch chéo có hoành độ có hoành độ \(x ≥ 1\), tung độ \(y\) tùy ý.
Vậy số phức có phần thực lớn hơn hoặc bằng \(-1\) có điểm biểu diễn ở hình 71.a (SGK)
b) Trên hình 71.b(SGK), điểm biểu diễn có tung độ \(y ∈ [1, 2]\), hoành độ \(x\) tùy ý.
Vậy số phức có phần ảo thuộc đoạn \([-1, 2]\)
c) Trên hình 71.c (SGK), hình biểu diễn \(z\) có hoành độ \(x ∈ [-1, 1]\) và \(x^2+y^2≤ 4\) (vì \(|z| ≤ 4\)).
Vậy số phức có phần thực thuộc đoạn \([-1, 1]\) và môdun không vượt quá \(2\).

