Bài 2.9: Tìm đạo hàm của các hàm số sau:
\(y = x\sqrt {1 + {x^2}} .\)
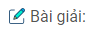
\(y’ = {{1 + 2{x^2}} \over {\sqrt {1 + {x^2}} }}.\)
Bài 2.10: Tìm đạo hàm của hàm số sau:
\(y = {\left( {a + {b \over x} + {c \over {{x^2}}}} \right)^4}\) (a,b,c là các hằng số).
Advertisements (Quảng cáo)
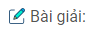
\(y = – 4{\left( {a + {b \over x} + {c \over {{x^2}}}} \right)^3}\left( {{b \over {{x^2}}} + {{2c} \over {{x^3}}}} \right).\)
Bài 2.11: Tìm đạo hàm của hàm số sau:
Advertisements (Quảng cáo)
\(y = \sqrt {{x^3} – 2{x^2} + 1} .\)
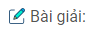
\(y’ = {{3{x^2} – 4x} \over {2\sqrt {{x^3} – 2{x^2} + 1} }}.\)
Bài 2.12: Rút gọn:
\(f\left( x \right) = \left( {{{x – 1} \over {2\left( {\sqrt x + 1} \right)}} + 1} \right).{2 \over {\sqrt x + 1}}:{\left( {{{\sqrt {x – 2} } \over {\sqrt {x + 2} + \sqrt {x – 2} }} + {{x – 2} \over {\sqrt {{x^2} – 4} – x + 2}}} \right)^2}\) và tìm f'(x)
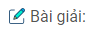
\(f\left( x \right) = {4 \over {{x^2} – 4}};{\rm{ }}f’\left( x \right) = – {{8x} \over {{{\left( {{x^2} – 4} \right)}^2}}}.\)

