Câu 17. Tìm mệnh đề đúng trong các mệnh đề sau đây:
a. Hai đường thẳng chéo nhau thì không có điểm chung
b. Hai đường thẳng không có điểm chung thì chéo nhau
c. Hai đường thẳng không song song thì chéo nhau
d. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau
a. Mệnh đề đúng.
b. Mệnh đề sai (xét trường hợp hai đường thẳng song song)
c. Mệnh đề sai (xét hai đường thẳng cắt nhau)
d. Mệnh đề đúng.
Câu 18. Cho tứ diện ABCD. Gọi M, N là hai điểm phân biệt cùng thuộc đường thẳng AB; P, Q là hai điểm phân biệt cùng thuộc đường thẳng CD. Xét vị trí tương đối của hai đường thẳng MQ, NP và vị trí tương đối của hai đường thẳng MP, NQ
Hai đường thẳng MQ và NP chéo nhau.
Thật vậy, giả sử chúng không chéo nhau, tức chúng cùng thuộc một mp(\(\alpha\)) nào đó. Vậy M, N, P, Q cùng thuộc mp(\(\alpha\)) và do đó A, B, C, D cùng thuộc mp(\(\alpha\)). Điều này mâu thuẫn với giả thiết ABCD là một tứ diện.
Chứng minh tương tự, hai đường thẳng MP và NQ cũng chéo nhau.
Câu 19. Cho tứ diện ABCD. Bốn điểm P, Q, R, S lần lượt nằm trên bốn cạnh AB, BC, CD, DA và không trùng với các đỉnh của tứ diện. Chứng minh rằng
a. Bốn điểm P, Q, R, S đồng phẳng khi và chỉ khi ba đường thẳng PQ, RS, AC hoặc đôi một song song hoặc đồng quy
b. Bốn điểm P, Q, R, S đồng phẳng khi và chỉ khi ba đường thẳng PS, RQ, BD hoặc đôi một song song hoặc đồng quy
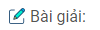
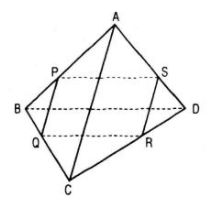
a. Nếu P, Q, R, S đồng phẳng thì chúng cùng thuộc mặt phẳng (PQRS).
Ta có:
(PQRS) ∩ (ABC) = PQ
(PQRS) ∩ (ACD) = RS
(ABC) ∩ (ACD) = AC
Advertisements (Quảng cáo)
Theo định lí về giao tuyến của ba mặt phẳng thì PQ, SR, AC hoặc đôi một song song hoặc đồng quy.
Ngược lại, nếu ba đường thẳng PQ, AC, RS hoặc đôi một song song hoặc đồng quy thì hai đường thẳng PQ và RS cùng thuộc một mặt phẳng, từ đó bốn điểm P, Q, R, S đồng phẳng.
Câu 20. Cho tứ diện ABCD và ba điểm P, Q, R lần lượt nằm trên ba cạnh AB, CD, BC. Hãy xác định giao điểm S của mp(PQR) với cạnh AD nếu:
a. PR // AC
b. PR cắt AC
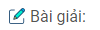
a. Trường hợp PR // AC
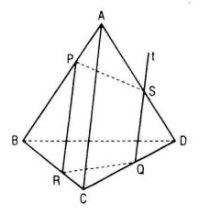
Hai mặt phẳng (PQR) và (ACD) có điểm chung Q và lần lượt chứa hai đường thẳng song song PR và AC nên :
(PQR) ∩ (ACD) = Qt // AC
Gọi {S} = Qt ∩ AD thì {S} = AD ∩ (PQR)
b. Trường hợp PR cắt AC
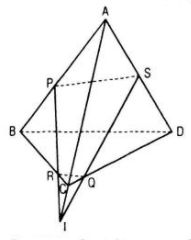
Giả sử {I} = PR ∩ AC
⇒ (PQR) ∩ (ACD) = QI
Trong mp(ACD) ta có
Advertisements (Quảng cáo)
{S} = QI ∩ AD thì {S} = AD ∩ (PQR)
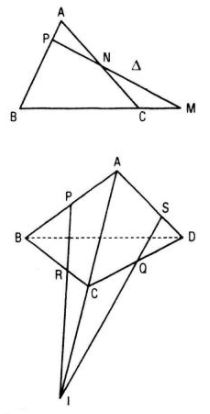
Câu 21. Cho tứ diện ABCD. Các điểm P, Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp(PQR) và cạnh AD. Chứng minh rằng AS = 2SD
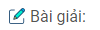
Định lí Menelaus
Giả sử đường thẳng Δ cắt các cạnh (hoặc
phần kéo dài) BC, CA, AB lần lượt tại M, N, P thì :
\({{MB} \over {MC}}.{{NC} \over {NA}}.{{PA} \over {PB}} = 1\)
Áp dụng định lí để giải bài toán
Gọi {I} = PR ∩ AC
Trong mp(ACD) goi {S} = QI ∩ AD
Thì {S} = AD ∩ (PQR)
Áp dụng định lí Menelaus trong tam giác ABC
với cát tuyến PRI ta có
\({{PA} \over {PB}}.{{RB} \over {RC}}.{{IC} \over {IA}} = 1 \Rightarrow 1.2.{{IC} \over {IA}} = 1\)
\( \Rightarrow {{IC} \over {IA}} = {1 \over 2}\) ⇒ C là trung điểm của AI.
Áp dụng định lí Menelaus trong tam giác ACD
với cát tuyến IQS ta có :
\({{IC} \over {IA}}.{{QD} \over {QC}}.{{SA} \over {SD}} = 1 \Rightarrow {1 \over 2}.1.{{SA} \over {SD}} = 1 \)
\(\Rightarrow SA = 2SD\,\,\left( {dpcm} \right)\)
Câu 22. Gọi G là trọng tâm của tứ diện ABCD
a. Chứng minh rằng đường thẳng đi qua G và một đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy
b. Gọi A’ là trọng tâm của mặt BCD. Chứng minh rằng GA = 3GA’
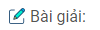
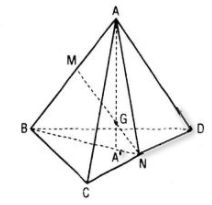
a. Trong mp(ABN) gọi A’ là giao điểm của AG với trung tuyến BN của ΔBCD. Ta chứng minh :
A’B = 2A’N
Áp dụng định lí Menelaus trong ΔBMN với cát tuyến AGA’ ta có :
\({{AM} \over {AB}}.{{GN} \over {GM}}.{{A’B} \over {A’N}} = 1 \Rightarrow {1 \over 2}.1.{{A’B} \over {A’N}} = 1 \Rightarrow A’B = 2A’N\)
Vậy A’ là trọng tâm của ΔBCD
Tương tự BG ,CG, DG lần lượt đi qua trọng tâm B’, C’, D’ của tam giác ACD, ABD, ABC.
b. Chứng minh GA = 3GA’
Áp dụng định lí Menelaus trong ΔABA’ với cát tuyến MGN ta có :
\({{MA} \over {MB}}.{{GA’} \over {GA}}.{{NB} \over {NA’}} = 1 \Rightarrow 1.{{GA’} \over {GA}}.3 = 1 \)
\(\Rightarrow GA = 3GA’\,\,\left( {dpcm} \right)\)

