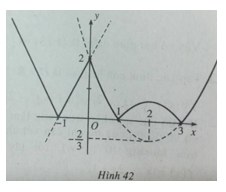
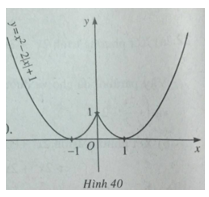
Bài 23: Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {x^2} – 2\left| x \right| + 1\)

Tập xác định của hàm số là D = R. Ngoài ra \(f( – x) = {( – x)^2} – 2| – x| + 1 = {x^2} – 2|x| + 1 = f(x)\)
Hàm số là hàm số chẵn. Đồ thị của nó nhận trục tung làm trục đối xứng. Để xét chiều biến thiên và vẽ đồ thị của nó chỉ cần xét chiều biến thiên và vẽ đồ thị của nó trên nửa khoảng \({\rm{[}}0; + \infty )\) , rồi lấy đối xứng qua Oy. Với \(x \ge 0\) có \(f(x) = {x^2} – 2x + 1\)
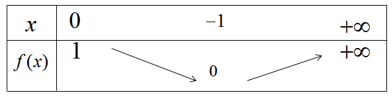
Bảng biến thiên
Đồ thị của hàm số đã cho được vẽ ở hình 40.
Advertisements (Quảng cáo)
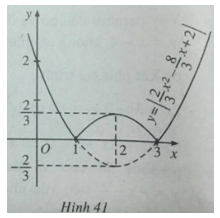
Bài 24: Vẽ đồ thị của hàm số \(y = \left| {{2 \over 3}{x^2} – {8 \over 3}x + 2} \right|\)

Vì \(\left| {f(x)} \right| = \left\{ \matrix{f(x),f(x) \ge 0 \hfill \cr – f(x),f(x) < 0 \hfill \cr} \right.\)
Nên để vẽ đồ thị của hàm số y = |f(x)| ta vẽ đồ thị của hàm số y =f(x), sau đó giữ nguyên phần đồ thị ở phía trên trục hoành và lấy đối xứng phần đồ thị nằm phía dưới trục hoành qua trục hoành.
Advertisements (Quảng cáo)
Trong trường hợp này, ta vẽ đồ thị của hàm số \(y = {2 \over 3}{x^2} – {8 \over 3}x + 2\) , sau đó giữ nguyên phần đồ thị ứng với các nửa khoảng \(( – \infty ;1]\) và \({\rm{[}}3; + \infty )\) . Lấy đối xứng phần đồ thị ứng với khoảng (1;3) qua trục hoành.
Đồ thị của hàm số \(y = \left| {{2 \over 3}{x^2} – {8 \over 3}x + 2} \right|\) được vẽ trên hình 41 (đường nét liền)
Bài 25: Cho hàm số
\(y = f(x) = \left\{ \matrix{
{2 \over 3}{x^2} – {8 \over 3}x + 2,x > 0 \hfill \cr
2x + 2,x \le 0 \hfill \cr} \right.\)
Vẽ đồ thị của hàm số \(y = \left| {f(x)} \right|\)

Với x >0 ta có đồ thị của y = |f(x)| như hình 41 (bỏ phần ứng với \(x \le 0\) )
Với \(x \le 0\) , trước hết vẽ đồ thị hàm số y = 2x + 2. Giữ yên phần đồ thị đoạn [-1;0], bỏ đi phần đồ thị ứng với khoảng \(( – \infty ; – 1)\) , thay vào đó là phần đối xứng với phần bỏ đi qua trục hoành. Đồ thị hàm số y = f|(x)| được vẽ trên hình 42 (đường nét liền).