Bài 15: Tam giác \(ABC\) có \(a = 12, b = 13, c = 15\). Tính \(\cos A\) và góc \(A\).

Áp dụng công thức tính ta có
\(\eqalign{
& \cos A = {{{b^2} + {c^2} – {a^2}} \over {2bc}} = {{{{13}^2} + {{15}^2} – {{12}^2}} \over {2.13.15}} = {{25} \over {39}} \cr
& \Rightarrow \,\,\widehat A \approx {50^0} \cr} \)
Bài 16: Cho tam giác \(ABC\) có \(AB = 5,\,AC = 8,\,\widehat A = {60^0}\). Kết quả nào trong các kết quả sau là độ dài cạnh \(BC\) ?
a) \(\sqrt {129} \); b) \(7\);
c) \(49\); d) \(\sqrt {69} \).

Ta có \(B{C^2} = {a^2} = {b^2} + {c^2} – 2bc.\cos A = {8^2} + {5^2} – 2.8.5.\cos {60^0} = 49\)
\( \Rightarrow \,\,BC = 7\).
Chọn b).
Advertisements (Quảng cáo)
Bài 17: Hình 59 vẽ một hồ nước nằm ở góc tạo bởi hai con đường. Bốn bạn An, Cường , Trí, Đức dự đoán khoảng cách từ B đến C như sau
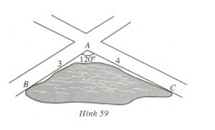
An : \(5 km\)
Cường : \(6 km\)
Trí : \(7 km\)
Đức : \(5,5 km\).
Advertisements (Quảng cáo)
Biết rằng khoảng cách từ \(A\) đến \(B\) là \(3 km\), khoảng cách từ \(A\) đến \(C\) là \(4 km\), góc \(BAC\) là \({120^0}\).
Hỏi dự đoán của bạn nào sát với thực tế nhất ?

Áp dụng định lí cosin ta có
\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos \widehat {BAC} = {3^2} + {4^2} – 2.3.4.\cos {120^0} \cr
& \,\,\,\,\,\,\,\,\,\,\,\;\ = 9 + 16 + 12 = 37 \cr
& \Rightarrow BC = \sqrt {37} \approx 6,1 \cr} \)
Vậy bạn Cường dự đoán sát với thực tế nhất.
Bài 18: Cho tam giác \(ABC\). Chứng minh các khẳng định sau
a) Góc \(A\) nhọn khi và chỉ khi \({a^2} < {b^2} + {c^2}\);
a) Góc \(A\) tù khi và chỉ khi \({a^2} > {b^2} + {c^2}\);
a) Góc \(A\) vuông khi và chỉ khi \({a^2} = {b^2} + {c^2}\).

Ta có \(\cos A = {{{b^2} + {c^2} – {a^2}} \over {2bc}}\)
a) \(A\) nhọn \( \Leftrightarrow \,\,\cos A > 0\,\, \Leftrightarrow \,\,{b^2} + {c^2} > {a^2}\).
b) \(A\) tù \( \Leftrightarrow \,\,\cos A < 0\,\, \Leftrightarrow \,\,{b^2} + {c^2} < {a^2}\) .
c) \(A\) vuông \( \Leftrightarrow \,\,\cos A = 0\,\, \Leftrightarrow \,\,{b^2} + {c^2} = {a^2}\) .

