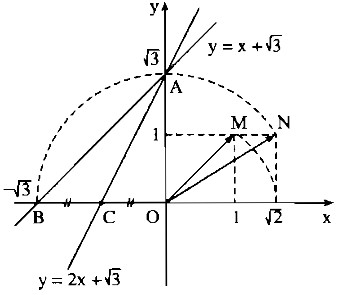
Câu 14: a) Vẽ đồ thị của các hàm số au trên cũng một mặt phẳng tọa độ
\(y = x + \qrt 3\); (1)
\(y = 2x + \qrt 3 \); (2)
b) Gọi giao điểm của đường thẳng \(y = x + \qrt 3 \) với các trục Oy, Ox theo thứ tự là A, B và giao điểm của đường thẳng \(y = 2x + \qrt 3 \) với các trục Oy, Ox theo thứ tự là A, C. Tính các góc của tam giác ABC (dùng máy tính bỏ túi CAIO fx-220 hoặc CAIO fx-500A).

a) *Vẽ đồ thị của hàm ố \(y = x + \qrt 3 \)
Cho x = 0 thì \(y = \qrt 3 \). Ta có: \(A\left( {0;\qrt 3 } \right)\)
Cho y = 0 thì \(x + \qrt 3 = 0 \Rightarrow x = – \qrt 3 \). Ta có: \(B\left( { – \qrt 3 ;0} \right)\)
Cách tìm điểm có tung độ bằng \(\qrt 3 \) trên trục Oy:
– Dựng điểm M(1;1). Ta có: \(OM = \qrt 2 \)
– Dựng cung tròn tâm O bán kính OM cắt trục Ox tại điểm có hoành độ bằng \(\qrt 2 \) .
– Dựng điểm \(N\left( {1;\qrt 2 } \right)\). Ta có: \(ON = \qrt 3 \)
– Vẽ cung tròn tâm O bán kính ON cắt trục Oy tại A có tung độ \(\qrt 3 \) cắt tia đối của Ox tại B có hoành độ \(-\qrt 3 \) .
Đồ thị của hàm ố \(y = x + \qrt 3 \) là đường thẳng AB.
*Vẽ đồ thị của hàm ố \(y = 2x + \qrt 3 \)
Cho x = 0 thì \(y = \qrt 3 \). Ta có: \(A\left( {0;\qrt 3 } \right)\)
Cho y = 0 thì \(2x + \qrt 3 = 0 \Rightarrow x = – {{\qrt 3 } \over 2}\). Ta có: \(C\left( { – {{\qrt 3 } \over 2};0} \right)\)
Đồ thị của hàm ố \(y = 2x + \qrt 3 \) là đường thẳng AC
b) Ta có: \(tg\widehat {ABO} = {{OA} \over {OB}} = {{\qrt 3 } \over {\qrt 3 }} = 1 \Rightarrow \widehat {ABO} = {45^0}\) hay \(\widehat {ABC} = {45^0}\)
\(tg\widehat {ACO} = {{OA} \over {OC}} = {{\qrt 3 } \over {{{\qrt 3 } \over 2}}} = 2 \Rightarrow \widehat {ACO} = {63^0}26’\)
Ta có: \(\widehat {ACO} + \widehat {ACB} = {180^0}\) (hai góc kề bù)
uy ra : \(\widehat {ACB} = {180^0} – \widehat {ACO} = {180^0} – {63^0}26′ = {116^0}34’\)
Lại có: \(\widehat {ACB} + \widehat {ABC} + \widehat {BAC} = {180^0}\)
uy ra:
\(\eqalign{
& \widehat {BAC} = {180^0} – \left( {\widehat {ACB} + \widehat {ABC}} \right) \cr
& = {180^0} – \left( {{{45}^0} + {{116}^0}34′} \right) = {18^0}26′ \cr} \)
Câu 15: Cho hàm ố \(y = \left( {m – 3} \right)x\)
a) Với các giá trị nào của m thì hàm ố đồng biến ? Nghịch biến ?
b) Xác định giá trị của m để đồ thị hàm ố đi qua điểm A(1;2).
c) Xác định giá trị của m để đồ thị hàm ố đi qua điểm B(1;-2).
d) Vẽ đồ thị của hai hàm ố ứng với giá trị của m tìm được ở các câu b) , c).

Điều kiện : \(m – 3 \ne 0 \Leftrightarrow m \ne 3\).
a) * Hàm ố đồng biến khi hệ ố \(a = m – 3 > 0 \Leftrightarrow m > 3\)
Vậy với m > 3 thì hàm ố \(y = \left( {m – 3} \right)x\) đồng biến.
* Hàm ố nghịch biến khi hệ ố \(a = m – 3 < 0 \Leftrightarrow m < 3\)
Vậy với m < 3 thì hàm ố \(y = \left( {m – 3} \right)x\) nghịch biến.
Advertisements (Quảng cáo)
b) Đồ thị của hàm ố \(y = \left( {m – 3} \right)x\) đi qua điểm A(1;2) nên tọa độ điểm A nghiệm
đúng phương trình hàm ố.
Ta có: \(2 = \left( {m – 3} \right)1 \Leftrightarrow 2 = m – 3 \Leftrightarrow m = 5\)
Giá trị m = 5 thỏa mãn điều kiện bài toán .
Vậy với m = 5 thì đồ thị hàm ố \(y = \left( {m – 3} \right)x\) đi qua điểm A(1;2)
c) Đồ thị của hàm ố \(y = \left( {m – 3} \right)x\) đi qua điểm B(1;-2) nên tọa độ điểm B nghiệm đúng phương trình hàm ố.
Ta có : \(- 2 = \left( {m – 3} \right)1 \Leftrightarrow – 2 = m – 3 \Leftrightarrow m = 1\)
Giá trị m = 1 thỏa mãn điều kiện bài toán .
Vậy với m = 1 thì đồ thị hàm ố \(y = \left( {m – 3} \right)x\) đi qua điểm B(1;-2).
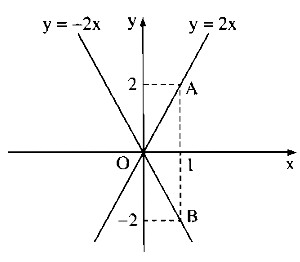
d) Khi m = 5 thì ta có hàm ố: y = 2x
Khi m = 1 thì ta có hàm ố: y = -2x
*Vẽ đồ thị của hàm ố y = 2x
Cho x = 0 thì y = 0. Ta có: O(0;0)
Cho x = 1 thì y = 2. Ta có: A(1;2)
Đường thẳng OA là đồ thị hàm ố y = 2x.
*Vẽ đồ thị của hàm ố
Cho x = 0 thì y = 0. Ta có : O(0;0)
Cho x = 1 thì y = -2 . Ta có : B(1;-2)
Đường thẳng OB là đồ thị của hàm ố y = -2x.
Câu 16: Cho hàm số \(y = \left( {a – 1} \right)x + a\)
a) Xác định giá trị của a để đồ thị hàm ố cắt trục tung tại điểm có tung độ bằng 2.
b) Xác định giá trị của a để đồ thị hám ố cắt trục tung tại điểm có hoành độ bằng -3
c) Vẽ đồ thị của hai hàm ố ứng với giá trị của a tìm được ở các câu a) , b) trên cùng hệ trục tọa độ Oxy và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.

Advertisements (Quảng cáo)
a) Hàm ố \(y = \left( {a – 1} \right)x + a\,\,\,\,\left( {a \ne 1} \right)\) là hàm ố bậc nhất có đồ thị hàm ố cắt trục tung
tại điểm có tung độ bằng y = 2 nên a = 2.
b) Hàm ố \(y = \left( {a – 1} \right)x + a\,\,\,\,\left( {a \ne 1} \right)\) là hàm ố bậc nhất có đồ thị hàm ố cắt trục hoành tại điểm có hoành độ x = -3 nên tung độ giao điểm này bằng 0.
Ta có:
\(\eqalign{
& 0 = \left( {a – 1} \right)\left( { – 3} \right) + a \cr
& \Leftrightarrow – 3x + 3 + a = 0 \cr
& \Leftrightarrow – 2a = – 3 \Leftrightarrow a = 1,5 \cr} \)
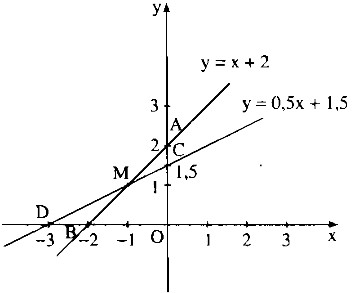
c) Khi a = 2 thì ta có hàm ố: y = x + 2
Khi a = 1,5 thì ta có hàm ố: \(y = 0,5x + 1,5\)
* Vẽ đồ thị của hàm ố \(y = x + 2\)
Cho x = 0 thì y = 2. Ta có: A(0;2)
Cho y = 0 thì x = -2. Ta có: B(-2;0)
Đường thẳng AB là đồ thị hàm ố \(y = x + 2\).
* Vẽ đồ thị của hàm ố \(y = 0,5x + 1,5\)
Cho x = 0 thì y = 1,5. Ta có: C(0;1,5)
Cho y = 0 thì x = -3. Ta có : B(-3;0)
Đường thẳng CD là đồ thị hàm ố \(y = 0,5x + 1,5\)
* Tọa độ giao điểm của hai đường thẳng .
Ta có: I thuộc đường thẳng \(y = x + 2\) nên \({y_1} = {x_1} + 2\)
I thuộc đường thẳng \(y = 0,5x + 1,5\) nên \({y_1} = 0,5{x_1} + 1,5\)
uy ra:
\(\eqalign{
& {x_1} + 2 = 0,5{x_1} + 1,5 \cr
& \Leftrightarrow 0,5{x_1} = – 0,5 \cr
& \Leftrightarrow {x_1} = – 1 \cr} \)
\({x_1} = – 1 \Rightarrow {y_1} = – 1 + 2 = 1\)
Vậy tọa độ giao điểm của hai đường thẳng là I(-1;1).
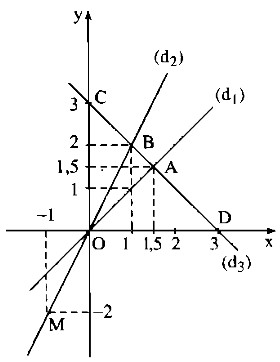
Câu 17: a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị các hàm số sau
y = x (d1) ;
y = 2x (d2);
y = -x + 3 (d3).
b) Đường thẳng (d3) cắt các đường thẳng (d1); (d2) theo thứ tự tại A, B.
Tìm tọa độ của các điểm A, B và tính diện tích tam giác OAB.

a) * Vẽ đồ thị của hàm ố y = x
Cho x = 0 thì y = 0
Cho x = 1 thì y = 1
Đồ thị hàm ố y = x là đường thẳng đi qua gốc tọa độ O(0;0) và điểm (1;1)
* Vẽ đồ thị của hàm ố y = 2x
Cho x = 0 thì y = 0
Cho x = 1 thì y = 2
Đồ thị hàm ố y = 2x là đường thẳng đi qua gốc tọa độ O(0;0) và điểm (1;2)
* Vẽ đồ thị của hàm ố y = -x + 3
Cho x = 0 thì y = 3. Ta có điểm (0;3)
Cho y = 0 thì x = 3. Ta có điểm (3;0)
Đồ thị hàm ố y = -x + 3 là đường thẳng đi qua hai điểm (0;3) và điểm (3;0)
b) * Gọi \(A\left( {{x_1};{y_1}} \right),\,\,B\left( {{x_2};{y_2}} \right)\), lần lượt là tọa độ giao điểm của đường thẳng (d3) với hai đường thẳng (d1); (d2).
Ta có: A thộc đường thẳng y = x nên \({y_1} = {x_1}\)
A thuộc đường thẳng y = -x + 3 nên \({y_1} = – {x_1} + 3\)
uy ra:
\(\eqalign{
& {x_1} = – {x_1} + 3 \cr
& \Leftrightarrow 2{x_1} = 3 \cr
& \Leftrightarrow {x_1} = 1,5 \cr} \)
\({x_1} = 1,5 \Rightarrow {y_1} = 1,5\)
Vậy tọa độ giao điểm của hai đường thẳng (d1) và (d2) là A(1,5;1,5).
Ta có: B thuộc đường thẳng y = 2x nên \({y_2} = 2{x_2}\)
B thuộc đường thẳng y = -x + 3 nên \({y_2} = – {x_2} + 3\)
uy ra :
\(\eqalign{
& 2{x_2} = – {x_2} + 3 \cr
& \Leftrightarrow 3{x_2} = 3 \cr
& \Leftrightarrow {x_2} = 1 \cr} \)
\({x_2} = 1 \Rightarrow {y_2} = 2\)
Vậy tọa độ giao điểm của hai đường thẳng (d1) và (d2) là B(1;2).

