Câu 28:
a) Vẽ trên cùng một mắt phẳng tọa độ đồ thị của các hàm số
y = -2x ; (1)
y = 0,5x ; (2)
b) Qua điểm K(0;2) vẽ đường thẳng (d) song song với trục Ox. Đường thẳng (d) cắt các đường thẳng (1) , (2) lần lượt tại A, B. Tìm tọa độ của các điểm A, B.
c) Hãy chứng tỏ rằng \9\widehat {AOB} = {90^0}\) (hai đường thẳng y = -2x và y = 0,5x vuông góc với nhau).

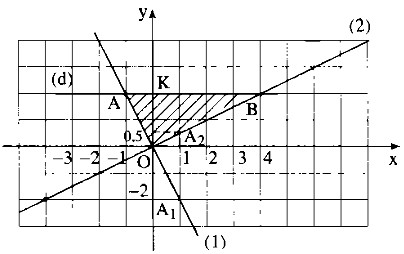
a) * Vẽ đồ thị hàm số y = -2x
Cho x = 0 thì y = 0. Ta có: O(0;0)
Cho x = 1 thì y = -2. Ta có : M(1;-2)
Đồ thị hàm số y = -2x đi qua điểm O và M.
* Vẽ đồ thị hàm số y = 0,5 x
Cho x = 0 thì y = 0 . Ta có : O(0;0)
Advertisements (Quảng cáo)
Cho x = 2 thì y = 1 . Ta có: N(2;1)
Đồ thị hàm số y = 0,5x đi qua O và N.
b) Đường thẳng (d) song song với trục Ox và đi qua điểm K(0;2) nên nó là
đường thẳng y = 2
Đường thẳng y = 2 cắt đường thẳng (1) tại A nên điểm A có tung độ bằng 2.
Thay y = 2 vào phương trình y = -2x ta được x = -1.
Vậy điểm A(-1;2)
Đường thẳng y = 2 cắt đường thẳng (2) tại B nên điểm B có tung độ bằng 2.
Thay y = 2 vào phương trình y = 0,5x ta được x = 4
Advertisements (Quảng cáo)
Vậy điểm B(4;2)
c) Xét hai tam giác vuông OAK và BOK , ta có:
\(\eqalign{
& \widehat {OKA} = \widehat {OKB} = {90^0} \cr
& {{AK} \over {OK}} = {1 \over 2};{{OK} \over {KB}} = {2 \over 4} = {1 \over 2} \cr
& \Rightarrow {{AK} \over {OK}} = {{OK} \over {KB}} \cr} \)
Suy ra \(\Delta OAK\) đồng dạng với \(\Delta BOK\)
Suy ra: \(\widehat {KOA} = \widehat {KOB}\)
Mà \(\widehat {KBO} + \widehat {KOB} = {90^0}\)
Suy ra: \(\widehat {KOB} = \widehat {KOB} = {90^0}\) hay \(\widehat {AOB} = {90^0}\).
Câu 29: Cho hàm số \(y = mx + \left( {2m + 1} \right)\) (1)
Với mỗi giá trị của \(m \in R\) , ta có một đường thẳng xác định bởi (1) . Như vậy, ta có một họ đường thẳng xác định bởi (1). Chứng minh rằng với mọi giá trị của m, họ đường thẳng xác định bởi (1) luôn đi qua một điểm cố định. Hãy xác định tọa độ của điểm đó.

Chứng minh họ đường thẳng \(y = mx + \left( {2m + 1} \right)\) (1) luôn đi qua một điểm cố định nào đó.
Giả sử điểm \(A\left( {{x_0};{y_0}} \right)\) là điểm mà họ đường thẳng (1) đi qua với mọi m.
Khi đó tọa độ điểm A nghiệm đúng phương trình hàm số (1).
Với mọi m , ta có: \({y_0} = m{x_0} + \left( {2m + 1} \right) \Leftrightarrow \left( {{x_0} + 2} \right)m + \left( {1 – y} \right) = 0\)
Vì phương trình nghiệm đúng với mọi giá trị của m nên tất cả các hệ số phải bằng 0.
Suy ra:
\(\eqalign{
& {x_0} + 2 = 0 \Leftrightarrow {x_0} = – 2 \cr
& 1 – {y_0} = 0 \Leftrightarrow {y_0} = 1 \cr} \)
Vậy A(-2;1) là điểm cố định mà họ đường thẳng \(y = mx + \left( {2m + 1} \right)\) luôn đi qua với mọi giá trị m.

