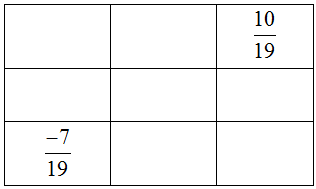
Câu 54: Cho hình vuông gồm 9 ô. Hãy sắp xếp các phân số sau đây vào các ô trống sao cho trong mỗi hàng các phân số tăng dần từ trái sang phải và trong mỗi cột, các phân số tăng dần từ trên xuống dưới:
$${9 \over {19}};{{ – 25} \over {19}};{{20} \over {19}};{{42} \over {19}};{{30} \over {19}};{{14} \over {19}};{{ – 13} \over {19}}$$
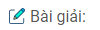
Ta có: \({{ – 25} \over {19}} < {{ – 13} \over {19}} < {9 \over {19}} < {{14} \over {19}} < {{20} \over {19}} < {{30} \over {19}} < {{42} \over {19}}\)
Ở cột thứ nhất phân ô cuối cùng là \({{ – 7} \over {19}}\) mà trong cột các phân số tăng từ trên xuống dưới nên dòng thứ nhất điền \({{ – 25} \over {19}}\), dòng thứ 2 là \({{ – 13} \over {19}}\)
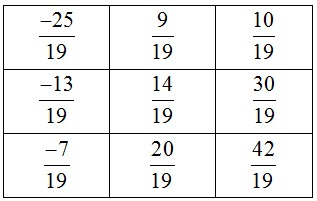
Ở dòng thứ nhất ô cuối cùng là \({{10} \over {19}}\). Trong mỗi dòng các phân số tăng từ trái sang phải nên ô thứ 2 điền \({9 \over {19}}\)
Để cho cột thứ 2 và thứ 3 tăng từ trên xuống, dòng 2 và dòng 3 tăng từ trái sang phải, cột 2 ta điền \({{14} \over {19}};{{20} \over {19}}\); cột thứ 3 điền \({{30} \over {19}};{{42} \over {19}}\) hoặc dòng thứ 2 điền \({{14} \over {19}}\) và \({{20} \over {19}}\) dòng thứ 3 điền \({{30} \over {19}};{{42} \over {19}}\)
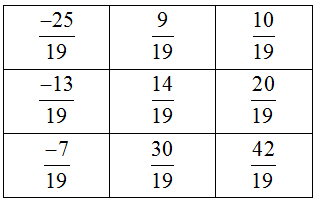
Câu 55: Cũng yêu cầu như bài 54 với các phân số:
$${1 \over 3};{1 \over 5};{{ – 2} \over {15}};{1 \over 6};{{ – 2} \over { – 5}};{{ – 1} \over {10}};{4 \over {15}}$$

Advertisements (Quảng cáo)
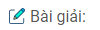
\({1 \over 3} = {{10} \over {30}};{1 \over 5} = {6 \over {30}};{{ – 2} \over {15}} = {{ – 4} \over {30}};{1 \over 6} = {5 \over {30}};\)
\({{ – 2} \over { – 5}} = {{12} \over {30}};{{ – 1} \over {10}} = {{ – 3} \over {30}};{4 \over {15}} = {8 \over {30}}\)
\({3 \over {10}} = {9 \over {30}};{{ – 1} \over {15}} = {{ – 2} \over {30}};\)
\({{ – 4} \over {30}} < {{ – 3} \over {30}} < {{ – 2} \over {30}} < {5 \over {30}} < {6 \over {30}} < {8 \over {30}} < {9 \over {30}} < {{10} \over {30}} < {{12} \over {30}}\)
Suy ra:
\({{ – 2} \over {15}} < {{ – 1} \over {10}} < {{ – 1} \over {15}} < {1 \over 6} < {1 \over 5} < {4 \over {15}} < {3 \over {10}} < {1 \over 3} < {{ – 2} \over { – 5}}\)
Ở dòng thứ nhất ô cuối cùng là \({3 \over {10}}\). Trong mỗi dòng các phân số tăng từ trái sang phải nên ô thứ 2 điền \({1 \over 6}\)
Advertisements (Quảng cáo)
Để cho cột thứ 2 và thứ 3 tăng từ trên xuống, dòng 2 và dòng 3 tăng từ trái sang phải, cột 2 ta điền \({1 \over 5}\); \({1 \over 3}\) cột thứ 3 điền \({4 \over 15}\); \({-2 \over -5}\).
Ta có bảng sau:
: Câu 56
Cho hai phân số \({{ – 3} \over 8}\) và \({{ – 2} \over 5}\). Chỉ cần so sánh hai tích (-3).5 và 8.(-2), ta cũng có thể kết luận được rằng \({{ – 3} \over 8} > {{ – 2} \over 5}\). Em có thể giải thích được không? Hãy phát biểu và chứng minh cho trường hợp tổng quát khi so sánh hai phân số \({a \over b}\) và \({c \over d}\) (a, b, c, d ∈ Z, b>0, d>0)
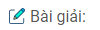
Vì \({{ – 3} \over 8} = {{( – 3).5} \over {8.5}};{{ – 2} \over 5} = {{( – 2).8} \over {5.8}}\)
(-3).5 > (-2).8 Vậy \({{ – 3} \over 8} > {{ – 2} \over 5}\)
Với hai phân số \({a \over b}\) và \({c \over d}\) (a, b, c, d ∈ Z, b>0, d>0) \({a \over b} > {c \over d}\) thì ad > bc và ngược lại.
Chứng minh: \({a \over b} = {{a{\rm{d}}} \over {b{\rm{d}}}};{c \over d} = {{bc} \over {b{\rm{d}}}}\)
Ta có: \({a \over b} > {c \over d}\) Suy ra \({{a{\rm{d}}} \over {b{\rm{d}}}} > {{bc} \over {b{\rm{d}}}}\). Theo quy tắc so sánh hai phân số ta có: ad > bc
Ngược lại: \({a \over b} = {{a{\rm{d}}} \over {b{\rm{d}}}};{c \over d} = {{bc} \over {b{\rm{d}}}}\)
Ta có ad > bc. Theo quy tắc so sánh hai phân số
Suy ra: \({{a{\rm{d}}} \over {b{\rm{d}}}} > {{bc} \over {b{\rm{d}}}}\). Suy ra \({a \over b} > {c \over d}\)
Câu 57: Điền số nguyên thích hợp vào ô vuông:
$${{ – 8} \over {15}} < {{…} \over {40}} < {{ – 7} \over {15}}$$
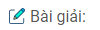
\({{ – 8} \over {15}} < {{…} \over {40}} < {{ – 7} \over {15}}\) Suy ra \({{ – 64} \over {120}} < {{3 …} \over {120}} < {{ – 56} \over {120}}\)
Số nguyên điền vào ô trống là: -21; -20; -19.

