Câu 5: Vẽ hai đường thẳng xx’ và yy’ cắt nhau tại điểm O. Hãy đo một góc rồi suy ra số đo các góc còn lại. Nói rõ cách lí luận.
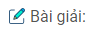
Giả sử trong hình dưới, hai đường thẳng xx’ và yy’ cắt nhau tại O, góc xOy bằng 110°
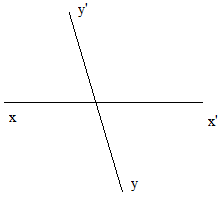
Ta có \(\widehat {xOy} = \widehat {x’Oy’}\) (hai góc đối đỉnh)
\( \Rightarrow \widehat {x’Oy’} = 110^\circ \)
\(\widehat {xOy} + \widehat {x’Oy’} = 180^\circ \) (hai góc kề bù)
\( \Rightarrow \widehat {x’Oy’} = 180^\circ – \widehat {xOy} = 180^\circ – 110^\circ = 70^\circ \)
\(\widehat {xOy’} = \widehat {x’Oy}\) (hai góc đối đỉnh)
\( \Rightarrow \widehat {x’Oy} = 70^\circ \)
Câu 6: Hai đường thẳng MN và PQ cắt nhau tại A tạo thành góc MAP có số đo bằng \(33^\circ \).
a) Tính số đo góc NAQ.
Advertisements (Quảng cáo)
b) Tính số đo góc MAQ.
c) Viết tên các cặp góc đối đỉnh.
d) Viết tên các cặp góc bù nhau.
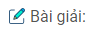
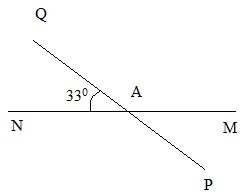
a) Ta có:
Advertisements (Quảng cáo)
\(\widehat {NAQ}\) và \(\widehat {PAM}\) là hai góc đối đỉnh
Suy ra: \(\widehat {NAQ} = \widehat {PAM}\)
Mà \(\widehat {PAM} = 33^\circ \) nên \(\widehat {NAQ} = 33^\circ \)
b) \(\widehat {PAM}\) và \(\widehat {MAQ}\) là hai góc kề bù nên \(\widehat {PAM} + \widehat {MAQ} = 180^\circ \)
Suy ra: \(\widehat {MAQ} = 180^\circ – \widehat {PAM} = 180^\circ – 33^\circ = 147^\circ \)
c) Các cặp góc đối đỉnh là \(\widehat {PAM}\) và \(\widehat {NAQ}\); \(\widehat {PAN}\) và \(\widehat {MAQ}\)
d) Các cặp góc kề bù nhau là:
\(\widehat {PAM}\) và \(\widehat {MAQ}\); \(\widehat {PAM}\) và \(\widehat {PAN}\);
\(\widehat {NAQ}\) và \(\widehat {PAN}\); \(\widehat {NAQ}\) và \(\widehat {QAM}\).
Câu 7: Trong hai câu sau. Câu nào đúng? Câu nào sai? Hãy bác bỏ câu sai bằng hình vẽ.
a) Hai góc đối đỉnh thì bằng nhau.
b) Hai góc bằng nhau thì đối đỉnh.
a) Câu a đúng vì theo đình nghĩa hai góc đối đỉnh.
b) Câu b sai vì hai góc bằng nhau chưa chắc đối đỉnh nhau.
Hình vẽ: