Bài 62: Giải và biện luận các hệ phương trình
a)
\(\left\{ \matrix{
x + y = 4 \hfill \cr
xy = m \hfill \cr} \right.\)
b)
\(\left\{ \matrix{
3x – 2y = 1 \hfill \cr
{x^2} + {y^2} = m \hfill \cr} \right.\)
a) Theo định lý Vi-ét đảo, x và y là nghiệm của hệ phương trình:
z2 – 4z + m = 0 (1)
Ta có: Δ’ = 4 – m
Do đó:
+ Nếu m > 4 thì Δ’ < 0 thì phương trình (1) vô nghiệm nên hệ đã cho vô nghiệm
+ Nếu m = 4 thì Δ’ = 0 thì phương trình (1) có một nghiệm kép z = 2 nên hệ đã cho có một nghiệm duy nhất \((x, y) = (2, 2)\)
+ Nếu m < 4 thì Δ’ > 0 thì phương trình (1) có hai nghiệm phân biệt \(z = 2 \pm \sqrt {4 – m} \) nên hệ đã cho có hai nghiệm:
\(\left\{ \matrix{
x = 2 – \sqrt {4 – m} \hfill \cr
y = 2 + \sqrt {4 – m} \hfill \cr} \right. \text{ và } \left\{ \matrix{
x = 2 + \sqrt {4 – m} \hfill \cr
y = 2 – \sqrt {4 – m} \hfill \cr} \right.\)
b) Ta có:
\(\left\{ \matrix{
3x – 2y = 1 \hfill \cr
{x^2} + {y^2} = m \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2y = 3x – 1 \hfill \cr
4{x^2} + 4{y^2} = 4m \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
2y = 3x – 1 \hfill \cr
4{x^2} + {(3x – 1)^2} = 4m \hfill \cr} \right.\)
Advertisements (Quảng cáo)
Xét riêng phương trình 4x2 + (3x – 1)2 = 4m ⇔ 13x2 – 6x – 4m + 1= 0 (2)
Phương trình (2) có biệt thức thu gọn Δ’ = 4(13m – 1).
Do đó:
+ Nếu \(m < {1 \over {13}} \Rightarrow \Delta ‘ < 0\) , phương trình (2) vô nghiệm nên hệ vô nghiệm.
+ Nếu \(m = {1 \over {13}} \Rightarrow \Delta ‘ = 0\) , phương trình (2) có một nghiệm \(x = {3 \over {13}}\) nên hệ có nghiệm là
+ Nếu \(m > {1 \over {13}} \Rightarrow \Delta ‘ > 0\) thì phương trình (2) có hai nghiệm: \({x_{1,2}} = {{3 \pm 2\sqrt {13m – 1} } \over {13}}\) , nên hệ có hai nghiệm như sau:
\(\eqalign{
& ({x_1},{y_1}) = ({{3 – 2\sqrt {13m – 1} } \over {13}};\,{{ – 2 – 3\sqrt {13m – 1} } \over {13}}) \cr
& ({x_2},{y_2})\, = \,({{3 + 2\sqrt {13m – 1} } \over {13}};\,{{ – 2 + 3\sqrt {13m – 1} } \over {13}}) \cr} \)
Bài 63: Tìm a, b và c để Parabol y = ax2 + bx + c có đỉnh là I(1; -4) và đi qua điểm M(2; -3). Hãy vẽ Parabol nhận được.
\(I(1, -4)\) là đỉnh của Parabol nên:
Advertisements (Quảng cáo)
\(\left\{ \matrix{
– {b \over {2a}} = 1 \hfill \cr
– 4 = a + b + c \hfill \cr} \right.\)
\(M(2, -3)\) thuộc parabol nên: \(-3 = 4a + 2b + c\)
Ta có hệ:
\(\left\{ \matrix{
2a + b = 0 \hfill \cr
a + b + c = – 4 \hfill \cr
4a + 2b + c = – 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 1 \hfill \cr
b = – 2 \hfill \cr
c = – 3 \hfill \cr} \right.\)
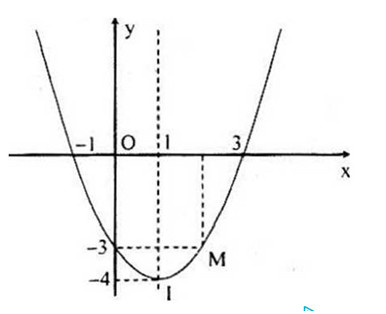
Vậy \(y = x^2 – 2x – 3\)
Đồ thị hàm số: \(y = x^2 – 2x – 3\)
Bài 64: Cho tam giác ABC có BC = a; AC = b; AB = c.Ta lấy một điểm M trên cạnh BC. Quy M, ta kẻ các đường thẳng ME và MF thứ tự song song với các cạnh AC và AB (E ∈ AB, F ∈ AC). Hỏi phải lấy điểm M cách B bao nhiêu để tổng ME + MF = l(l là độ dài cho trước)? Biện luận theo l, a, b và c
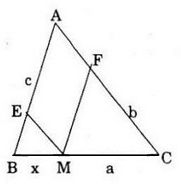
Đặc x = MB (điều kiện: 0 < x < a)
Theo định lý Ta – lét, ta có:
\(\eqalign{
& {{ME} \over x} = {b \over a} \Rightarrow ME = {{bx} \over a} \cr
& {{MF} \over c} = {{a – x} \over a} \Rightarrow MF = {{c(a – x)} \over a} \cr} \)
Điều kiện \(ME + MF = l\) cho ta phương trình:
\(l = {{bx} \over a} + {{c(a – x)} \over a} \Leftrightarrow (b – c)x = a(l – c)\,\,(1)\)
+ Nếu b = c (tức là tam giác ABC cân tại A) thì phương trình (1) vô nghiệm nếu \(l ≠ c\); nghiệm đúng với mọi x nếu \(l = c\). Điều này có nghĩa là:
_ Khi tam giác ABC cân tại A và \(l ≠ AB\) thì không có điểm M nào trên cạnh BC thỏa mãn điều kiện của tam giác.
– Khi tam giác ABC cân tại A và \(l = AB\) thì mọi điểm M nằm trên cạnh BC đều thỏa mãn điều kiện của tam giác.
+ Nếu b ≠ c (tức là tam giác ABC không cân ở A), thì phương trình (1) có một nghiệm duy nhất \(x = {{a(l – c)} \over {b – c}}\) .
Xét điều kiện 0 < x < a:
\(0 < x < a \Leftrightarrow 0 < {{a(l – c)} \over {b – c}} < a \Leftrightarrow 0 < {{l – c} \over {b – c}} < 1\,\,(2)\)
Với b ≠ c nên có hai trường hợp:
+ Với b > c, ta có: (2) \(⇔ 0 < l – c < b – c ⇔ c < l < b\)
+ Với b < c, ta có: (2) \(⇔ 0 > l – c > b – c ⇔ c > l > b\)
Hai kết quả trên có nghĩa là giá trị \(x = {{a(l – c)} \over {b – c}}\) là nghiệm của bài toán ( điểm M cách B một khoảng bằng \( {{a(l – c)} \over {b – c}}\) khi và chỉ độ dài \(l\) nằm giữa các độ dài b và c)

