Bài 1: Một ô tô đang chuyển động thẳng với vận tốc 72 km /h thì giảm đều tốc độ cho đến khi dừng lại. Biết rằng sau quãng đường 50m, vận tốc giảm đi còn một nửa
a) Tính gia tốc của xe.
b) Quãng đường đi được từ lúc vận tốc còn một nửa cho đến lúc xe dừng hẳn là bao nhiêu ?
Giải :
Chọn gốc tọa độ O ở vị trí bắt đầu giảm vận tốc , chiều dương là chiều chuyển động , gốc thời gian (t0 = 0) là lúc bắt đầu giảm vận tốc thì \({v_0} = 72\,km/h = 20\,m/s\,;\)
\({S_1} = \Delta x = 50\,m;{v_1} = {{{v_0}} \over 2} = 10\,(m/s)\)
a) \(a = {{v_1^2 – v_0^2} \over {2\Delta x}} = {{{{10}^2} – {{20}^2}} \over {2.50}} = – 3(m/{s^2})\)
b) Khi dừng hẳn : v2 = 0
Quãng đường đi còn lại :
\({S_2} = {{v_2^2 – v_1^2} \over {2a}} = {{ – {{10}^2}} \over {2.( – 3)}} = 16,7(m)\)
Bài 2: Một người thợ xây ném một viên gạch theo phương thẳng đứng cho một người khác ở trên tầng cao 4m. Người này chỉ việc giơ tay ngang ra là bắt được viên gạch . Hỏi vận tốc khi ném là bao nhiêu để cho vận tốc viên gạch lúc người kia bắt được bằng 0 ?
Giải :
Khoảng cách từ điểm ném đến điểm bắt gạch là 4m ; Vận tốc gạch tại điểm bắt v = 0
Chọn chiều dương hướng lên thì :
\(\eqalign{ & h = \Delta x = {{ – v_0^2} \over {2a}} = {{ – v_0^2} \over {2( – g)}} = {{v_0^2} \over {2g}} \cr & {v_0} = \sqrt {2gh} = \sqrt {2.9,8.4} = 8,85(m/s) \cr} \)
Bài 3: Người ta ném một vật từ mặt đất lên trên cao theo phương thẳng đứng với vận tốc 4,0 m/s . Hỏi sau bao lâu thì vật đó rơi chạm đất ? Độ cao cực đại vật đạt được bao nhiêu ? Vận tốc khi chạm đất là bao nhiêu ?
Advertisements (Quảng cáo)
Giải
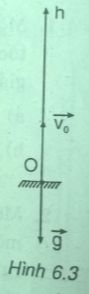
Chọn hệ tọa độ như hình 6.3 , gốc thời gian là lúc ném thì
\({v_0} = 4,0(m/s);a = – g = – 9,8(m/{s^2})\)
Phương trình chuyển động : \(h = 4t – 4,9{t^2}(s;m)\)
Biểu thức vận tốc : v = 4 – 9,8t (s;m)
a) Khi chạm đất : h= 0
\(t(4 – 4,9t) = 0 < = > \left[ \matrix{ t = 0\text{ (lúc bắt đầu ném)}. \hfill \cr t = 0,82(s) \hfill \cr} \right.\)
Sau t = 0,82 s thì vật chạm đất
Advertisements (Quảng cáo)
b) Tại vị trí cao nhất : \(v = 0 = > h = {{ – v_0^2} \over {2a}} = {{v_0^2} \over {2g}} = {{{4^2}} \over {2.9,8}} \approx 0,82(m)\)
c) Vật chạm đất : \(v = 4 – 9,8.0,82 \approx – 4,04(m/s)\)
Bài 4: Một máy bay chở khách muốn cất cánh được phải chạy trên đường băng dài 1,8 km để đạt vận tốc 300 km/h . Hỏi máy bay phải có gia tốc không đổi tối thiểu bao nhiêu ?
Giải
Chọn chiều dương là chiều chuyển động để :
\(\Delta x = S;v = 300km/h = 83,3m/s\)
Độ dài quãng đường lớn nhất máy bay có thể đi trước khi cất cánh :
\({S_{{\rm{max}}}} = 1,8\,km = 1800m\)
Điều kiện về quãng đường :
\(S \le {S_{{\rm{max}}}} < = > {{{v^2}} \over {2a}} \le {S_{{\rm{max}}}} \)
\(< = > a \ge {{{v^2}} \over {2{S_{{\rm{max}}}}}} = {{{{83,3}^2}} \over {2.1800}} \approx 1,93(m/{s^2})\)
Gia tốc tối thiểu : \({a_{\min }} = 1,93(m/{s^2})\)
Bài 5: Một đoàn tàu rời ga chuyển động nhanh dần đều với gia tốc 0,1 m/s2 trên đoạn đường 500 m, sau đó thì chuyển động đều . Hỏi sau 1 h tàu đi được quãng đường bằng bao nhiêu ?
Giải :
Chọn gốc tọa độ tại ga , chiều dương là chiều chuyển động : \(\Delta x = S\)
Vận tốc của chuyển động thẳng đều là vận tốc cuối của đoạn đường tăng tốc S1 nên :
\(2a{S_1} = {v^2} – v_0^2 = {v^2} \)
\(= > v = \sqrt {2a.{S_1}} = \sqrt {2.0,1.500} = 10(m/s)\)
Thời gian tăng tốc : \({t_1} = {v \over a} = {{10} \over {0,1}} = 100(s)\)
Thời gian chuyển động thẳng đều cho tới thời điểm 1 h :
\({t_2} = 1h – 100s = 3500s\)
Quãng đường đi được sau 1 h :
\(S = {S_1} + {S_2} = 500 + 10.3500\)
\(= 35500(m) = 35,5\,(km)\)

