Bài 23: Gọi \(H\) là trực tâm của tam giác không vuông \(ABC\). Chứng minh rằng bán kính các đường tròn ngoại tiếp các tam giác \(ABC,\,HBC,\,HCA,\,HAB\) bằng nhau.

Trường hợp 1: Tam giác \(ABC\) có ba góc nhọn.
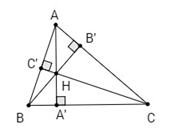
Gọi \(R,\,{R_1}\) lần lượt là bán kính đường tròn ngoại tiếp tam giác \(ABC, HBC\).
Áp dụng định lí sin ta có
\({{BC} \over {\sin A}} = 2R\,;\,\,{{BC} \over {\sin \widehat {BHC}}} = 2{R_1}\)
Mà \(\widehat {BHC} + \widehat A = \widehat {{B’}H{C’}} + \widehat A = {180^0}\) (Vì \(\widehat {BHC}\) và \(\widehat {{B’}H{C’}}\) đối đỉnh)
\( \Rightarrow \,\,\sin A = \sin \widehat {BHC}\)
Do đó \(2R = 2{R_1}\,\, \Rightarrow \,\,R = {R_1}.\)
Vậy bán kính đường tròn ngoại tiếp tam giác \(HBC\) bằng bán kính đường tròn ngoại tiếp tam giác \(ABC\).
Advertisements (Quảng cáo)
Tương tự bán kính đường tròn ngoại tiếp tam giác \(HCA, HAB\) bằng bán kính đường tròn ngoại tiếp tam giác \(ABC\).
Trường hợp 2: Tam giác \(ABC\) có góc tù.
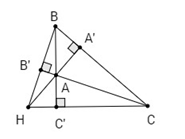
Ta có \({{BC} \over {\sin \widehat{BAC}}} = 2R\,;\,\,{{BC} \over {\sin \widehat {BHC}}} = 2{R_1}\)
Mà \(\widehat {B’AC’} + \widehat {CHB} = {180^0}\,\, \Rightarrow \,\,\sin \widehat{BAC} =\sin \widehat{B’AC’}= \sin \widehat {CHB}\) (Vì \(\widehat{BAC}\) và \(\widehat{B’AC’}\) đối đỉnh)
\( \Rightarrow \,\,R = {R_1}\)
Advertisements (Quảng cáo)
Tương tự ta chứng minh được bán kính đường tròn ngoại tiếp tam giác \(HCA, HAB\) bằng bán kính đường tròn ngoại tiếp tam giác \(ABC\).
Bài 24: Tam giác \(ABC\) có \(a = 7,\,b = 8,\,c = 6\). Tính \({m_a}\).

Áp dụng công thức tính \({m_a}\) ta có
\({m_a}^2 = {{{b^2} + {c^2}} \over 2} – {{{a^2}} \over 4} = {{{8^2} + {6^2}} \over 2} – {{{7^2}} \over 4} = {{151} \over 4}\,\,\,\, \Rightarrow \,{m_a} \approx 6,1\)
Bài 25: Tam giác \(ABC\) có \(a = 5,\,b = 4,\,c = 3\). Lấy điểm \(D\) đối xứng với \(B\) qua \(C\). Tính độ dài \(AD\).

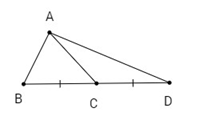
Áp dụng công thức tính trung tuyến \(AC\) trong tam giác \(ABD\) ta có
\(A{C^2} = {{A{B^2} + A{D^2}} \over 2} – {{B{D^2}} \over 4}\,\,\, \Rightarrow \,\,{4^2} = {{{3^2} + A{D^2}} \over 2} – {{{{10}^2}} \over 4}\,\,\, \Rightarrow \,A{D^2} = 73\,\,\, \Rightarrow \,AD = \sqrt {73} \approx 8,5.\)
Bài 26: Cho hình bình hành \(ABCD\) có \(AB = 4,\,BC = 5,\,BD = 7\). Tính \(AC\).

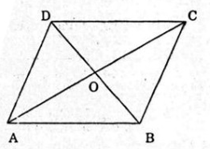
Gọi \(O\) là tâm hình bình hành.
Áp dụng công thức tính trung tuyến \(AO\) của tam giác \(ABD\), ta có
\(\eqalign{
& A{O^2} = {{A{B^2} + A{D^2}} \over 2} – {{B{D^2}} \over 4}\,\,\, = {{{4^2} + {5^2}} \over 2} – {{{7^2}} \over 4} = {{33} \over 4}\,\,\,\cr& \Rightarrow \,AO = \sqrt {{{33} \over 4}} = {{\sqrt {33} } \over 2} \cr
& \Rightarrow \,AC = 2AO = \sqrt {33} \approx 5,8 \cr} \)

