Bài 19: Tam giác \(ABC\) có \(\widehat A = {60^0},\,\widehat B = {45^0},\,b = 4\). Tính hai cạnh \(a\) và \(c\).

Ta có \(\widehat C = {180^0} – \widehat A – \widehat B = {180^0} – {60^0} – {45^0} = {75^0}\)
Áp dụng định lí sin ta có
\(\eqalign{
& {a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}} = {4 \over {{\mathop{\rm s}\nolimits} {\rm{in4}}{5^0}}} \cr
& {a \over {\sin {{60}^0}}} = {4 \over {{\mathop{\rm s}\nolimits} {\rm{in4}}{5^0}}}\,\,\,\, \Rightarrow \,\,a = 4.{{\sqrt 3 } \over 2}.\sqrt 2 = 2\sqrt 6 \cr
& {c \over {{\mathop{\rm s}\nolimits} {\rm{in7}}{{\rm{5}}^0}}} = {4 \over {{\mathop{\rm s}\nolimits} {\rm{in4}}{5^0}}}\,\,\,\, \Rightarrow \,\,\,c \approx \,5,5 \cr} \)
Bài 20: Cho tam giác \(ABC\) có \(\widehat A = {60^0},\,a = 6\). Tính bán kính đường tròn ngoại tiếp tam giác.

Ta có \({a \over {\sin A}} = 2R\,\, \Rightarrow \,\,R = {a \over {2\sin A}} = {6 \over {2.\sin {{60}^0}}} = {6 \over {\sqrt 3 }} = 2\sqrt 3 \, \approx 3,5\)
Advertisements (Quảng cáo)
Bài 21: Chứng minh rằng nếu ba góc của tam giác \(ABC\) thỏa mãn hệ thức \(\sin A = 2\sin B.\cos C\) thì \(ABC\) là tam giác cân.

Áp dụng định lí sin và cosin ta có
\(\sin A = {a \over {2R}},\,\,\sin B = {b \over {2R}},\,\,\cos C = {{{a^2} + {b^2} – {c^2}} \over {2ab}}\)
Advertisements (Quảng cáo)
Do đó \(\sin A = 2\sin B\cos C\,\,\, \Leftrightarrow \,\,{a \over {2R}} = 2.{b \over {2R}}.{{{a^2} + {b^2} – {c^2}} \over {2ab}}\,\,\,\)
\( \Leftrightarrow \,\,{a^2} = {a^2} + {b^2} – {c^2}\,\,\, \Leftrightarrow \,\,b^2 = c^2\, \Leftrightarrow \,\,b=c\)
Vậy \(ABC\) là tam giác cân.
Bài 22: Hình 60 vẽ một chiếc tàu thủy đang neo đậu ở vị trí \(C\) trên biển và hai người ở các vị trí quan sát \(A\) và \(B\) cách nhau \(500m\). Họ đo được góc \(CAB\) bằng \({87^0}\) và góc \(CBA\) bằng \({62^0}\).
Tính các khoảng cách \(AC\) và \(BC\).
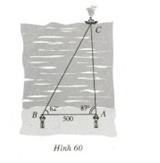

Ta có \(\widehat {ACB} = {180^0} – {87^0} – {62^0} = {31^0}\)
Áp dụng định lí sin ta có
\({a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}} = {{500} \over {{\mathop{\rm s}\nolimits} {\rm{in3}}{{\rm{1}}^0}}} \approx 971\)
\( \Rightarrow \,\,BC = a = 971.\sin {87^0} \approx 969\) m và \(\,AC = b = 971.\sin {62^0} \approx 857\) m.

