Bài 8: Chứng minh rằng điều kiện cần và đủ để tam giác \(ABC\) vuông tại \(A\) là \(\overrightarrow {BA} .\,\overrightarrow {BC} = A{B^2}\).

Ta có \(\overrightarrow {BA} .\,\overrightarrow {BC} = {\overrightarrow {BA} ^2}\,\, \Leftrightarrow \,\,\overrightarrow {BA} (\overrightarrow {BC} – \overrightarrow {BA} ) = 0\)
\( \Leftrightarrow \overrightarrow {BA} .\,\overrightarrow {AC} = 0\,\, \Leftrightarrow \,\,BA \bot AC\)
\( \Leftrightarrow \) Tam giác \(ABC\) vuông tại \(A\).
Bài 9: Cho tam giác \(ABC\) với ba đường trung tuyến \(AD, BE, CF\). Chứng minh rằng
\(\overrightarrow {BC} .\overrightarrow {AD} + \overrightarrow {CA} .\overrightarrow {BE} + \overrightarrow {AB} .\overrightarrow {CF} = 0\).

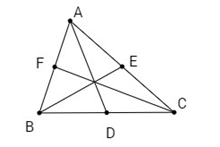
Ta có \(\overrightarrow {AD} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {AC} )\)
\(\eqalign{
& \overrightarrow {BE} = {1 \over 2}(\overrightarrow {BA} + \overrightarrow {BC} ) \cr
& \overrightarrow {CF} = {1 \over 2}(\overrightarrow {CA} + \overrightarrow {CB} ) \cr} \)
Advertisements (Quảng cáo)
Do đó \(\overrightarrow {BC} .\overrightarrow {AD} + \overrightarrow {CA} .\overrightarrow {BE} + \overrightarrow {AB} .\overrightarrow {CF} \)
\(\eqalign{
& = {1 \over 2}\overrightarrow {BC} (\overrightarrow {AB} + \overrightarrow {AC} ) + {1 \over 2}\overrightarrow {CA} (\overrightarrow {BA} + \overrightarrow {BC} ) + {1 \over 2}\overrightarrow {AB} (\overrightarrow {CA} + \overrightarrow {CB} ) \cr
& = {1 \over 2}(\overrightarrow {BC} \overrightarrow {AB} + \overrightarrow {BC} \overrightarrow {AC} + \overrightarrow {CA} \overrightarrow {BA} + \overrightarrow {CA} \overrightarrow {BC} + \overrightarrow {AB} \overrightarrow {CA} + \overrightarrow {AB} \overrightarrow {CB} )\cr
& = {1 \over 2}(\overrightarrow {BC} \overrightarrow {AB} + \overrightarrow {AB} \overrightarrow {CB} ) + {1 \over 2}(\overrightarrow {BC} \overrightarrow {AC} + \overrightarrow {CA} \overrightarrow {BC} ) + {1 \over 2}(\overrightarrow {CA} \overrightarrow {BA} + \overrightarrow {AB} \overrightarrow {CA} ) = 0 \cr} \)
(điều phải chứng minh)
Bài 10: Cho hai điểm \(M, N\) nằm trên đường tròn đường kính \(AB = 2R\). Gọi \(I\) là giao điểm của hai đường thẳng \(AM, BN\).
a) Chứng minh rằng \(\overrightarrow {AM} .\overrightarrow {AI} = \overrightarrow {AB} .\overrightarrow {AI} \,\,;\,\,\overrightarrow {BN} .\overrightarrow {BI} = \overrightarrow {BA} .\overrightarrow {BI}.\)
b) Tính \(\overrightarrow {AM} .\overrightarrow {AI} + \,\,\overrightarrow {BN} .\overrightarrow {BI} \) theo \(R\).
Advertisements (Quảng cáo)

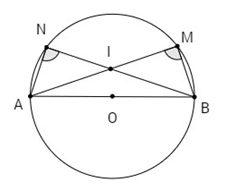
a) Ta có \(\overrightarrow {AM} .\,\overrightarrow {AI} = (\overrightarrow {AB} + \overrightarrow {BM} ).\,\overrightarrow {AI} = \overrightarrow {AB} .\,\overrightarrow {AI} + \overrightarrow {BM} .\,\overrightarrow {AI} = \overrightarrow {AB} .\,\overrightarrow {AI} \) ( vì \(\overrightarrow {BM} .\,\overrightarrow {AI} = 0\) ).
Tương tự, \(\overrightarrow {BN} .\,\overrightarrow {BI} = (\overrightarrow {BA} + \,\overrightarrow {AN} ).\,\overrightarrow {BI} = \overrightarrow {BA} .\,\overrightarrow {BI} + \overrightarrow {AN} .\,\overrightarrow {BI} = \overrightarrow {BA} .\,\overrightarrow {BI} \) ( vì \(\overrightarrow {AN} .\,\overrightarrow {BI} = 0\) ).
b) Theo câu a), \(\overrightarrow {AM} .\overrightarrow {AI} + \overrightarrow {BN} .\overrightarrow {BI} = \overrightarrow {AB} .\overrightarrow {AI} \, + \overrightarrow {BA} .\overrightarrow {BI} \)
\( = \overrightarrow {AB} (\overrightarrow {AI} – \overrightarrow {BI} ) = \overrightarrow {AB} .\,\overrightarrow {AB} = A{B^2} = 4{R^2}.\)
Bài 11: Cho hai đường thẳng \(a\) và \(b\) cắt nhau tại \(M\). Trên \(a\) có hai điểm \(A\) và \(B\), trên \(b\) có hai điểm \(C\) và \(D\) đều khác \(M\) sao cho \(\overrightarrow {MA} .\overrightarrow {MB} = \overrightarrow {MC} .\overrightarrow {MD} \,\,\). Chứng minh rằng bốn điểm \(A, B, C, D\) cùng nằm trên một đường tròn.

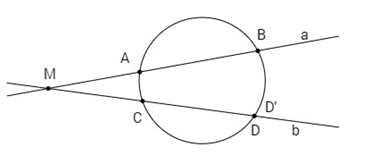
Gọi \((O)\) là đường tròn ngoại tiếp tam giác \(ABC\). Gọi \(D’\) là giao điểm của \(b\) với \((O)\) ( \({D’} \ne C\)).
Theo giả thiết ta có \(\overrightarrow {MA} .\overrightarrow {MB} = \overrightarrow {MC} .\overrightarrow {M{D’}} \,\,\)
\(\eqalign{
& \Rightarrow \,\,\overrightarrow {MC} .\overrightarrow {MD} = \overrightarrow {MC} .\overrightarrow {M{D’}} \cr
& \Rightarrow \,\,\overrightarrow {MC} (\overrightarrow {MD} – \overrightarrow {M{D’}} ) = 0 \cr
& \Rightarrow \,\,\overrightarrow {MC} .\,\overrightarrow {{D’}D} = 0\,\,\,\, \cr} \)
\(\Rightarrow \,\overrightarrow {{D’}D} = 0\) (Do \(M, C, D, D’\) cùng thuộc đường thẳng b)
\( \Rightarrow D \equiv {D’}\).
Vậy bốn điểm \(A, B, C, D\) cùng nằm trên một đường tròn.

